Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

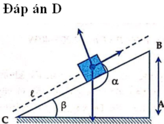
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có:
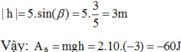

Đề bài không cho khối lượng nên mình cũng đang thắc mắc . Các bạn giúp mình nha.

1,
Cơ năng của vật tại vị trí thả
\(W_1=W_{đ1}+W_{t1}=mgh=0,4.10.20=80\)
thế năng ở vị trí C là
\(W_{t2}=0,4.10.15=60\)
theo định luật bảo toàn cơ năng có
\(W_{đ2}=W_{đ1}-W_{t2}=80-60=20\)

a) Bảo toàn năng lượng: \(mgh=\dfrac{1}{2}mv^2\Rightarrow v=...\)
b) Khi động năng bằng thế năng thì thế năng bằng một nửa cơ năng:\(mgh'=\dfrac{1}{2}mgh\Rightarrow h'=...\)
c) Dùng biến thiên động năng: \(0-\dfrac{1}{2}mv^2=\mu mg.s\Rightarrow s=...\)

Công của trọng lực chính bằng độ giảm thế năng
\(A=W_{t1}-W_{t2}=mgh-0=0,5.10.20=100\) J
(coi mốc thế năng tại chân dốc)
Áp dụng định luật bảo toàn cơ năng ta có
\(W_1=W_2\Rightarrow W_{t1}=W_{đ2}=100\) J
\(\Rightarrow v=\sqrt{\frac{2W_{đ2}}{m}}=\sqrt{\frac{2.100}{0,5}}=20\) m/s

Câu 2 :
a/\(Wt1−Wt2=m.g.z1−m.g.z2=m.g.(z1+z2)=3.10.(z1+z2)=30(z1+z2)(J)\)mà \(W_{t1}-W_{t2}=500-(-900)=1400(J)\Rightarrow Z=Z_{1}+Z_{2}=\frac{1400}{30}\approx 46,6(m)\)b/Tại vị trí ứng với mức thế năng bằng 0 thì z = 0
thế năng tại vị trí z1 là \(Wt1=m.g.z1⇒z1=5003.10≈16,6(m)\)
vậy vị trí ứng với mức không của thế năng đã chọn cách điểm thả vật 1 khoảng 16,6m
c)ta có
\(v2−v20=2.g.z1⇒v=2.g.z1√=2.10.16,6√=283√(m/s)\)

\(\overrightarrow{F}+\overrightarrow{F}_{ms}=\overrightarrow{N}+\overrightarrow{P}=m\overrightarrow{a}\)
Phương vuông góc mp nghiêng:
\(N=Pcos45\)
Phương mp nghiêng
\(F-F_{ms}=Psin45=ma\)
\(F=ma-F_{ms}+Psin45=14+0,2.10.1cos45+10.1sin45\)
\(=12,485N\)
 chúc Tết.
chúc Tết.
giải
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có: