Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
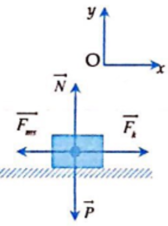
Theo định luật II Niu - tơn:
P → + N → + F k → + F m s → = m a →
Chiếu lên trục Oy:
N – P = 0 => N = P = m.g = 15.10 = 150 (N)
⇒ F m s = μ . N = 0,05.150 = 7,5 ( N )
Chiếu lên trục Ox:
F k − F m s = m . a ⇒ a = F k − F m s m = 45 − 7,5 15 = 2,5 ( m / s 2 )
Quãng đường vật đi được sau 5s là
S = 1 2 a . t 2 = 1 2 .2,5.5 = 2 31,25 m

\(\overrightarrow{F}+\overrightarrow{F}_{ms}=\overrightarrow{N}+\overrightarrow{P}=m\overrightarrow{a}\)
Phương vuông góc mp nghiêng:
\(N=Pcos45\)
Phương mp nghiêng
\(F-F_{ms}=Psin45=ma\)
\(F=ma-F_{ms}+Psin45=14+0,2.10.1cos45+10.1sin45\)
\(=12,485N\)

Gia tốc vật:
\(a=\dfrac{F_k}{m}=\dfrac{4}{2}=2\)m/s2
Sau khi đi được 9m kể từ lúc bắt đầu \(\left(v_0=0\right)\) thì vật đạt vận tốc: \(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS}=\sqrt{2\cdot2\cdot9}=6\)m/s

Gia tốc vật:
\(a=\dfrac{F_k}{m}=\dfrac{4}{2}=2\)m/s2
Sau khi đi được 9m thì vật đạt vận tốc:
\(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS+v^2_0}=\sqrt{2\cdot2\cdot9+0^2}=6\)m/s

theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F-Fms=0 (a=0, vật trượt đều) (2)
chiếu (1) lên trục Oy phương nằm ngang chiều dương hương lên trên
N=P=m.g (3)
từ (2),(3)
\(\Rightarrow\mu=\)0,2

Cơ năng ban đầu: \(W_1=mgh=mg.S.\sin30^0\)
Cơ năng ở chân mặt phẳng nghiêng: \(W_2=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W_1=W_2\)
\(\Rightarrow v=\sqrt{2gS.\sin 30^0}=\sqrt{2.10.10.\sin 30^0}=10(m/s)\)
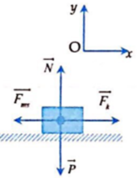

Chọn chiều (+) là chiều chuyển động của vật.
Vật được kéo trên mặt phẳng nằm ngang \(\Rightarrow N=P=mg=15.10=150\left(N\right)\)
Lực ma sát \(F_{ms}=\mu N=0,05.150=7,5\left(N\right)\)
Áp dụng định luật II Newton, ta có \(\overrightarrow{F}=m\overrightarrow{a}\) (1)
Chiếu (1) lên phương chuyển động của vật, ta có:
\(F_k-F_{ms}=ma\Rightarrow a=\dfrac{F_k-F_{ms}}{m}=\dfrac{45-7,5}{15}=2,5\left(m/s^2\right)\)
Vậy gia tốc của thùng là \(2,5m/s^2\).