Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
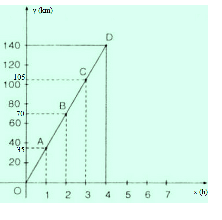
Ta có quãng đường đi được và thời gian là hai đại lượng tỉ lệ thuận.
Ta có công thức S = 35t.
Với t = 1 => S = 35 ta được A(1 ; 35) thuộc đồ thị.
Với S = 140 => t = 4 ta được B(4 ; 140) thuộc đồ thị.
Ta được đồ thị chuyển động là đoạn thằng OB như trên hình vẽ.

Hàm số biểu diễn sự phụ thuộc của quãng đường S vào thời gian t là: S = 35.t (km)
+ Chọn t = 4 ⇒ S = 35.4 = 140 (km)
⇒ D(4; 140) thuộc đồ thị hàm số.
Vậy đồ thị chuyển động là đoạn thẳng OD như hình vẽ dưới.

Hướng dẫn làm bài:
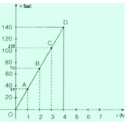
Ta có quãng đường đi được và thời gian là hai đại lượng tỉ lệ thuận.
Ta có công thức: S = 35.t
Với t = 1 =>S= 35 ta được A(1;35) thuộc đồ thị.
Với S = 140 => \(\Rightarrow t = {{140} \over {35}} = 4\) ta được B (4;140) thuộc đồ thị.
Ta được đồ thị chuyển động là đoạn thẳng OB như trên hình vẽ.

Hàm số biểu diễn sự phụ thuộc của quãng đường S vào thời gian t là: S = 35.t (km)
+ Chọn t = 4 ⇒ S = 35.4 = 140 (km)
⇒ D(4; 140) thuộc đồ thị hàm số.
Vậy đồ thị chuyển động là đoạn thẳng OD như hình vẽ dưới.

Nếu x là thời gian vận động viên đi được quãng đường y thì hàm số biểu thị sự chuyển động là: y = 35x
Ta có bảng giá trị sau:
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(\text{y=35.x}\) | \(35\) | \(70\) | \(105\) | \(140\) |
Đồ thị của chuyển động được biểu diễn trên hệ trục tọa độ Oxy như sau:


Đổi 3h6' = 31/10 h 31' = 31/60 h
Do lúc về t.gian về ít hơn 31/60 giờ
=> thời gian về: 31/10 - 31/60 = 31/12
gọi t.gian đi là x
=> thời gian về là 8 + x Ta có pt: 31 10 x = 31 12 (8 + x) <=> 31 10 x = 62 3 + 31 12 x
<=> 31 10 x - 31 12 x = 62 3
<=> 31 60 x = 62 3
<=> x = 40 S
= v . t
= 40 . 31 10 = 12,4km