K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

VT
31 tháng 8 2018
Chọn đáp án A
@ Lời giải:
+ Công thức xác định điện dung của tụ điện phẳng:
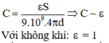
Nếu thay không khí bằng điện môi có hằng số điện môi là ε = 2 thì điện dung của tụ điện tăng lên 2 lần.

15 tháng 10 2017
a) tụ phẳng, điện môi không khí: C=S/4.pi.k.d . Thay số thôi, ở đây S là diện tích S=pi.r2=0,36pi,hằng số k=9.109Nm2/c2; khoảng cách giữa 2 bản d=2.10-3m. Ta được C=5.10-9 (F)
b) Qmax=C.Umax=C.E.d=5.10-9.3.106.2.10-3=3.10-5 (C); U=E.d=6.103(V)

VT
8 tháng 9 2018
+ Điện dung của tụ điện phẳng C ~ 1 d 2 → khi d tăng gấp đôi thì C giảm còn một phần tư → Đáp án B


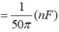
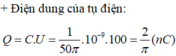

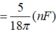



a) Thêm vào không gian giữa hai bản tấm kim loại có bề dày d < d0 như hình vẽ dưới ta thu được 2 tụ điện mắc nối tiếp nhau.
x d d 0 e e 0 0
Điện dung của mỗi tụ là
\(C_1=\frac{\varepsilon_0S}{4\pi kx}\)
\(C_2=\frac{\varepsilon_0S}{4\pi k\left(d_0-d-x\right)}\)
Khi đó độ tụ của bộ tụ này là
\(C=\frac{C_1C_2}{C_1+C_2}=\frac{\varepsilon_0S}{4\pi k}\left(\frac{1}{x\left(d_0-d-x\right)}:\left(\frac{1}{x}+\frac{1}{d_0-d-x}\right)\right)\)
\(=\frac{\varepsilon_0S}{4\pi k}\frac{1}{d_0-d}\).
b) Khi thay tấm kim loại thành tấm kim loại có hằng số điện môi \(\varepsilon\) , bề dày d , sau đó ép sát vào 2 mặt tấm điện môi hai bản kim loại mỏng thì lúc này sẽ có 3 tụ điện mắc nối tiếp như hình
x d d 0 e e e 0 0
\(C_1=\frac{\varepsilon_0S}{4\pi kx}\); \(C_2=\frac{\varepsilon S}{4\pi kd}\); \(C_3=\frac{\varepsilon_0S}{4\pi k\left(d-d_0-x\right)}\)
\(\Rightarrow C_{13}=\frac{C_1C_3}{C_1+C_3}=\frac{\varepsilon_0S}{4\pi k\left(d_0-d\right)}\)
\(\Rightarrow C_b=\frac{C_{13}C_2}{C_{13}+C_2}=\frac{S}{4\pi k}.\frac{\varepsilon\varepsilon_0}{d\left(d_0-d\right)}:\left(\frac{\varepsilon_0}{d_0-d}+\frac{\varepsilon}{d}\right)=\frac{S}{4\pi k}\frac{\varepsilon\varepsilon_0}{d\left(\varepsilon_0-\varepsilon\right)+\varepsilon d_0}.\)