Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Diện tích xung quanh của hình nón: ![]()
Cách giải:
Hình nón có đường sinh l = a và đáy ngoại tiếp tam giác đều cạnh a nên có bán kính 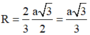
Vậy diện tích xung quanh của hình nón: 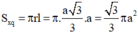

Đáp án D
Khối nón cần tìm có bán kính đáy r = a 2 2 ; chiều cao h = a .
Vậy diện tích xung quanh cần tính là S x q = π r l = π r h 2 + r 2 = 3 π a 2 2 .

Đáp án C.
Phương pháp:
Diện tích xung quanh của hình nón: S x q = π R l
Cách giải:
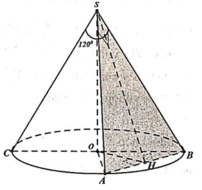
Gọi M là trung điểm AB ⇒ O M ⊥ A B . Mà O M ⊥ S O (vì SO vuông góc với đáy)
⇒ OM là đoạn vuông góc chung của SO và AB
⇒ d S O ; A B = O M = 3
Tam giác OMA vuông tại M:
O A 2 = O M 2 + M A 2 ⇒ R 2 = 3 2 + M A 2 ⇒ M A = R 2 − 9
Tam giác SAB vuông tại A có S A = S B (Vì Δ S O B = Δ S O A c . g . c )
⇒ Δ S A B vuông cân tại S
⇒ S A = A B 2 = 2 A M 2 = A M . 2 = 3 R 2 − 18
(N) có góc ở đỉnh là
120 0 ⇒ A S O = 60 0
Tam giác SOA vuông tại O:
sin O S A = O A S A ⇒ sin 60 0 = R 3 R 2 − 18 = 3 2 ⇒ 2 R = 3 . 3 R 2 − 18 ⇔ 4 R 2 = 6 R 2 − 54
⇔ R 2 = 27 ⇒ R = 3 3 .
l = S A = 2 R 2 − 18 = 2.27 − 18 = 36 = 6
S x q = π R l = π .3 3 .6 = 18 π 3
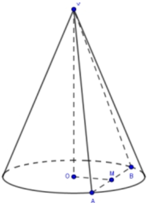


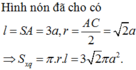

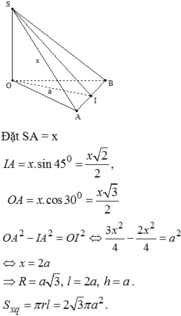

Hình nón có độ dài đường sinh l=SA=a; bán kính đáy
r = O A = 2 3 . a 3 2 = a 3 3 , có diện tích xung quanh là:
S x q = πrl = π . a 3 3 . a = πa 2 3 3
Chọn đáp án D.