Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Gọi x là số học sinh nam(x>0)
y là số học sinh nữ(y>0)
Ta có: \(\frac{x}{y}=\frac{3}{2}\) và x + y = 260
⇒\(\frac{x}{x+y}=\frac{3}{3+2}\)
⇒\(\frac{x}{260}=\frac{3}{5}\)
⇒x = 260.3/5 = 156(học sinh)
y = 260 - x = 260 - 156 = 104(học sinh)
vậy khối lớp 9 có 156 học sinh nam và 104 học sinh nữ
2.Gọi x là số học sinh lớp bán trú(x>0)
y là số học sinh lớp thường(y>0)
ta có \(\frac{x}{y}=\frac{2}{7}\) và x + y = 3600
⇒\(\frac{x}{x+y}=\frac{2}{2+7}\)
⇒\(\frac{x}{3600}=\frac{2}{9}\)
⇒x = 3600.2/9 = 800(học sinh)
y = 3600 - x = 3600 - 800 = 2800 (học sinh)
vậy trường có 800 học sinh ở lớp bán trú và 2800 học sinh ở lớp thường

Gọi số học sinh toàn trường đầu năm học là a học sinh (a ∈ N*)
Số học sinh nữ đầu năm học là a/ 2 học sinh.
Khi nhà trường nhận thêm 15 học sinh nữ và 5 học sinh nam thì số học sinh nữ là a/2 + 15 và số học sinh toàn trường là a + 20 học sinh.
Vì số học sinh nữ lúc này chiếm 51% số học sinh toàn trường nên ta có phương trình:
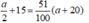
⇔ 50a + 1500 = 51a + 1020
⇔ a = 480 (thỏa mãn điều kiện a ∈ N*)
Vậy đến cuối kì I số học sinh nữ trong trường là 480: 2 + 15 = 255 học sinh, số học sinh nam là 480: 2 + 5 = 245 học sinh.

Số học sinh nữ của trường đó có là:
( 386 - 4) : 2 = 191 (học sinh)
Số học sinh nam của trường đó có là:
386 - 191 = 195 (học sinh)
số học sinh nam là
(386+4):2=195(h/s)
số học sinh nữ là
396-195=191(h/s)

Gọi số tăm mà lớp 8a đã mua là x (gói tăm) ( \(x\in N,x< 100\))
Vì lớp 8b mua đc nhiều hơn số tăm mà lớp 8a là 10 gói nên lớp 8b đã mua : x+10 (gói tăm)
Theo bài ra ta có lớp 8a và lớp 8b đã mua đc tất cả 100 gói tăm nên ta có phương trình :
\(x+\left(x+10\right)=100\Leftrightarrow2x=90\Leftrightarrow x=45\)(gói tăm ) (TM)
=> lớp 8b đã mua 55 gói tăm
Vậy lớp 8a đã mua 45 gói tăm
lớp 8b đã mua 55 gói tăm
gọi số hs nữ của khối 8 trường đó là x (hs)\(\left(x\in N,x< 162\right)\)
vì số hs nữ bằng 4/5 số hs nam nên số hs nam của khối 8 trường đó là : \(\dfrac{4}{5}x\) (hs)
theo bài ra thì khối 8 trường đó có 162 em nên ta có phương trình :
\(x+\dfrac{4}{5}x=162\Leftrightarrow\dfrac{9}{5}x=162\Leftrightarrow x=90\left(hs\right)\left(TM\right)\)
=> khối 8 đó có 72 hs nam
Vậy khối 8 đó có 90 hs nữ và 72 hs nam
Chúc bạn học tốt ^-^

Gọi số học sinh nữ là a, số học sinh nam là b
Ta có: a=b
=>a+b=a+a=2a
a+8=51%.(a+8+b+2)=51/100.(a+b+10)=51/100.(2a+10)
=> a+8=102/100.a+51/10
=>102/100.a-a=8-51/10
=> 1/50.a=29/10
=> a=29/10:1/50
=> a=145
=> a+b=2a=145.2=290
Vậy tổng số học sinh đầu năm là 290 học sinh.
Số phần của học sinh nữ là :
100% - 51% = 49 %
Trường có số học sinh là :
( 8 - 2 ) : ( 51 - 49 ) . 100 =300 ( học sinh )
Số học sinh đầu năm là :
300 - 8 - 2 = 290 (học sinh )
Đ/S : 290 học sinh

Gọi số học sinh khối 8 là \(x\)(học sinh). Điều kiện: \(x \in {\mathbb{N}^*};x < 580\).
Vì tổng số học sinh khối 8 và số học sinh khối 9 là 580 học sinh nên số học sinh khối 9 là \(580 - x\) (học sinh).
Khối 8 có số học sinh giỏi chiếm \(40\% \) số học sinh cả khối nên số học sinh giỏi khối 8 là \(40\% x = 0,4x\) (học sinh)
Khối 9 có số học sinh giỏi chiếm \(48\% \) số học sinh cả khối nên số học sinh giỏi khối 9 là \(48\% .\left( {580 - x} \right) = 0,48.\left( {580 - x} \right)\)
Vì cả hai khối có tổng cả 256 học sinh giỏi nên ta có phương trình:
\(0,4x + 0,48\left( {560 - x} \right) = 256\)
\(0,4x + 268,8 - 0,48x = 256\)
\(0,4x - 0,48x = 256 - 268,8\)
\( - 0,08x = - 12,8\)
\(x = \left( { - 12,8} \right):\left( { - 0,08} \right)\)
\(x = 160\) (thỏa mãn điều kiện)
Khi đó, số học sinh khối 9 là: \(560 - 160 = 400\) (học sinh)
Vậy khối 8 có 160 học sinh và khối 9 có 400 học sinh.
Gọi $x$ (học sinh) là số học sinh nữ của trường $(x∈N*)$
Số học sinh nam của trường là: $487-x$ (học sinh)
Số học sinh nữ sau khi tăng thêm là: $x+17$ (học sinh)
Số học sinh nam sau khi giảm là: $(100\%-10\%).(487-x)=0,9.(487-x)$ (học sinh)
Theo đề bài, ta có pt: $x+17+0,9.(487-x)=478$
$⇔x+17+438,3-0,9x=487$
$⇔0,1x=22,7$
$⇔x=227$ (nhận)
Vậy ban đầu trường đó có 227 học sinh nữ