Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
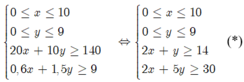
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

- Gọi số xe loại A và loại B cần dùng là x và y xe .
=> Số tiền là : \(T=4x+3y\)
Mà \(\left\{{}\begin{matrix}20x+10y\ge140\\0,6x+1,5y\ge9\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
Ta có :

a)
Nếu \(0 < x \le 2\) thì \(T(x) = 1,2x\) (triệu đồng)
Nếu \(x > 2\) thì \(T(x) = 1,2.2 + 0,9.(x - 2) = 0,9x + 0,6\) (triệu đồng)
Số tiền phải trả sau khi thuê x ngày là
\(T(x) = \left\{ \begin{array}{l}1,2x\quad \quad \quad \;(0 < x \le 2)\\0,9x + 0,6\quad (x > 2)\end{array} \right.\)
b) \(T(2) = 1,2.2=2,4\) (triệu đồng)
Ý nghĩa: số tiền khách phải trả khi thuê 2 ngày là 2,4 triệu đồng
\(T(3) = 0,9.3+0,6 = 3,3\) (triệu đồng)
Ý nghĩa: số tiền khách phải trả khi thuê 3 ngày là 3,3 triệu đồng
\(T(5) = 0,9.5+0,6=5,1\)
Ý nghĩa: số tiền khách phải trả khi thuê 5 ngày là 5,1 triệu đồng

Gọi số xe chở 3 tấn, chở 5 tấn và xe chở 7,5 tấn lần lượt là:\(x,y,z\left(x,y,z\in N;x,y,z>0\right)\).
Do tổng số xe là 57 nên: \(x+y+z=57\).
Số tấn xi măng phải chở là 290 tấn nên: \(3x+5y+7,5z=290\).
Tất cả số xe chở 7,5 tấn chở 3 chuyến được: \(3.7,5.z\).
Tất cả số xe 5 tấn chở 3 chuyến và số xe 3 tấn chở 2 chuyến được: \(3.5.y+2.3x\).
Ta có phương trình: \(3.7,5z=3.5y+2.3x\Leftrightarrow22,5z=15y+6x\)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y+z=57\\3x+5y+7,5z=290\\22,5z=15y+6x\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=19\\z=18\end{matrix}\right.\)
Vậy số xe 3 tấn là 20 xe, số xe 5 tấn là 19 chiếc, số xe 7,5 tấn là 18 xe.

Gọi x là số xe tải chở 3 tấn, y là số xe chở 5 tấn và z là số xe tải chở 7,5 tấn. Điều kiện x, y, z nguyên dương.
Theo giả thiết của bài toán ta có:
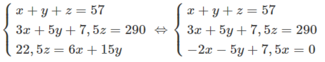
Cộng từng vế phương trình thứ hai với phương trình thứ ba ta được hệ phương trình
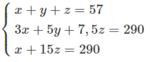
Nhân hai vế của phương trình thứ nhất với -5 rồi cộng từng vế với phương trình thứ hai ta được
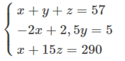
Từ phương trình cuối suy ra x = 290 – 15z
Thay giá trị tìm được của x vào phương trình thứ hai ta được 32,5z = 585 hay z = 18.
Từ đó suy ra x = 20, y = 19. Các giá trị của x, y, z vừa tìm được thỏa mãn điều kiện của bài toán.
Vậy có 20 xe chở 3 tấn, 19 xe chở 5 tấn và 18 xe chở 7,5 tấn.

Công ty A: \({y_A} = 3750 + 5.x\)(nghìn đồng)
Công ty B: \({y_B} = 2500 + 7,5.x\)(nghìn đồng)
Với \(550 \le x \le 600\)
Ta có:
\(\begin{array}{l}{y_A} - {y_B}=\left( {3750 + 5.x} \right) - \left( {2500 + 7,5x} \right)\\ = 1250 - 2,5x\end{array}\)
Mà \(550 \le x \le 600\)\( \Leftrightarrow 2,5.550 \le 2,5x \le 2,5.600\)
\(\begin{array}{l} \Leftrightarrow 1250 - 1370 \ge 1250 - 2,5x \ge - 250\\ \Leftrightarrow - 250 \le 1250 - 2,5x \le - 120\\ \Rightarrow {y_A} - {y_B} < 0\end{array}\)
Vậy chi phí thuê xe công ty A thấp hơn.
