Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số phần tử không gian mẫu là: C 40 4 = 91390 .
Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
C 10 2 . C 20 1 . C 10 1 + C 10 1 . C 20 2 . C 10 1 + C 10 1 . C 20 1 . C 10 2 = 37000
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 9 1 . C 6 1 + C 5 1 . C 9 2 . C 6 1 + C 5 1 . C 9 1 . C 6 2 = 2295
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 11 1 . C 4 1 + C 5 1 . C 11 2 . C 4 1 + C 5 1 . C 11 1 . C 4 2 = 1870
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
37000 - 2295 - 1870 = 32835
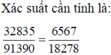

+ Không gian mẫu là kết quả của việc chọn ngẫu nhiên 3 học sinh trong số 10 học sinh
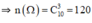
a) Gọi A: “ Cả ba học sinh chọn được đều là nam”
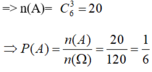
b) Gọi B: “ Trong 3 học sinh chọn được có ít nhất 1 nam”
⇒ B−: “ Cả ba học sinh được chọn đều là nữ”
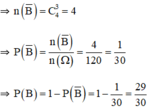

Đáp án: D.
![]()
Số cách chọn 3 học sinh có cả nam và nữ là
![]() .
.
Do đó xác suất để 3 học sinh được hcọn có cả nam và nữ là 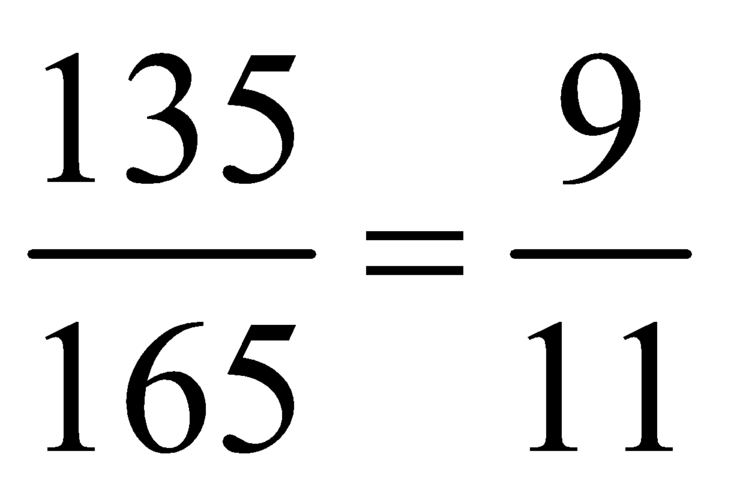 .
.

Gọi A là biến cố : "4 học sinh được chọn có đủ học sinh giỏi, học sinh khá và học sinh trung bình"
Số phần tử không gian mẫu \(\left|\Omega\right|=C^4_{33}=40920\)
Ta có các trường hợp được chọn sau :
(1) Có 2 học sinh giỏi, 1 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^2_{10}.C^1_{11}.C^1_{12}=5940\).
(2)Có 1 học sinh giỏi, 2 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^2_{11}.C^1_{12}=6600\).
(3)Có 1 học sinh giỏi, 1 học sinh khá và 2 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^1_{11}.C^2_{12}=7260\).
Ta được \(\left|\Omega_A\right|=5940+6600+7260=19800\)
Do đó : \(P\left(A\right)=\frac{\left|\Omega_A\right|}{\left|\Omega\right|}=\frac{15}{31}\)

Chọn B
Số cách chọn 2 học sinh trong 10 học sinh là C 10 2 .
Nên số phần tử của không gian mẫu là ![]() .
.
Gọi A : “ Biến cố chọn được hai học sinh đều là học sinh nữ”.
Số cách chọn 2 học sinh nữ trong 3 học sinh nữ là C 3 2 .
Khi đó số phần tử của biến cố A là n(A) = C 3 2 = 3.
Vậy xác suất để chọn được hai học sinh đều là nữ là 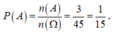

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()
Không gian mẫu: \(C_{12}^3\)
a. Số cách chọn 3 học viên đều khá: \(C_5^3\)
Xác suất: \(P=\dfrac{C_5^3}{C_{12}^3}=...\)
b. Số cách chọn sao cho không có học viên khá nào: \(C_7^3\)
\(\Rightarrow\) Số cách chọn có ít nhất 1 học viên khá: \(C_{12}^3-C_7^3\)
Xác suất: \(P=\dfrac{C_{12}^3-C_7^3}{C_{12}^3}\)