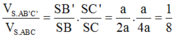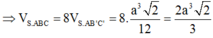NT Nguyễn Thị Thương Hoài (thuonghoaiquantri) 2025-08-23 22:07:26 Cô chào em, em có thể cho cô mượn 100 xu để trao tặng thành viên tích cực được không em? 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333) 2025-08-23 22:09:26 dạ nhưng em ko có xu ạ NT Nguyễn Thị Thương Hoài (thuonghoaiquantri) 2025-08-23 22:10:48 Lúc cô có cô sẽ trả lại em gấp đôi, em nhé! được không em? ...
Đọc tiếp
NT
Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:07:26 Cô chào em, em có thể cho cô mượn 100 xu để trao tặng thành viên tích cực được không em? 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:09:26 dạ nhưng em ko có xu ạ NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:10:48 Lúc cô có cô sẽ trả lại em gấp đôi, em nhé! được không em? 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:11:23 nhưng em đổi quà hết rồi 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:13:12 em chỉ còn 30 xu thôi ạ em cô chuyển cho em 50 xu xog em chuyển lại 30 xu tổng là em sẽ chuyển 80 xu ạ NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:13:53 được rồ, cô chuyển cho em 50 xu nhé, xong em cho cô mượn 80 xu nhé! 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:14:16 dạ vâng xong em chuyển cả luôn ạ NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:15:14 Rồi đó em! 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:16:07 em chưa nhận được cô 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:16:25 vẫn là 30xu cô ạ NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:17:23 rồi mà em NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:17:28 em xem lại đi em 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:18:40 cô đi lừa đảo em hay em đi lừa đảo cô vậy:) NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:19:44 cô chuyển 50 xu thật rồi mà em 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:20:50 ý là định đi lừa đảo ai v bn NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:21:04 Trả cô 50 xu mau lên 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:21:09 có làm thì mới có ăn xu này tôi sẽ chuyển vào nick thật của cô hoài 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:21:15 đừng hòng NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:21:28 50 xu là của tôi 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:21:45 ? 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:22:22 ko nghe:) NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:22:24 Em có thể trả lại cho cô 50 xu được không? 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:22:43 em chuyển cho cô hoài tht rồi:) 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:24:40 lừa ai chứ ko lừa được thằng này đâu cô fake ạ NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:26:34 thôi tao đéo cần NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:27:06 tao đã lừa được 2 người rồi, haha 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:27:44 ghê v pro 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:28:00 nhưng tôi chỉ cs 1730 xu th:) NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:28:12 PM Phạm Minh Hiếu (thuonghoaiquantri) 2025-08-20 12:22:09 vâng ạ 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:28:30 ? NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:28:31 PM Phạm Minh Hiếu (thuonghoaiquantri) 2025-08-20 12:22:53 Em chuyển rồi ạ NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:28:53 tao đùa đấy NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:28:58 không phải nó đâu 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:29:17 tôi đag chat vs cô hoài trên zalo đây 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:29:35 sáng mai pro chuẩn bị tinh thần mất nick thật đi nhé:) NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:29:44 TA ⋆౨ৎ˚ ࣪ᴇʙᴇ_ʙắᴘ♪⟡˖ (khanhpham.111981@gmail.com) 2025-08-23 22:19:59 Em chuyển rồi, bao giờ cô trả ạ? NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:30:13 tao lập nick khác,, haha NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:30:30 tao sẽ chuyển 550 xu sang điện thoại tao NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:30:32 haha 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:31:41 chuyển sang đt kiểu j NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:32:07 dễ thôi, tao đã lâp 2 nick rồi, 1 máy tính 1 điện thoại NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:32:09 haha NT Nguyễn Thị Thương Hoài (thuonghoaiquantri)
2025-08-23 22:32:37 và tao sẽ lừa đứa tiếp theo 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:33:02 tốt r 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:33:07 m thì hay r 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:33:30 cô hoài đag đọc chat của t vs m và ng bị lừa đã lên tiếng trên hỏi đáp r ok 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:36:21 đủ 1k xu mới rút dc ra cơ bé kph lo 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:36:45 admin và các ctv sẽ sớm tìm ra và sau đó sẽ phơi bày trc tất cả mn 𝙈𝙖𝙣𝙘𝙝𝙚𝙨𝙩𝙚𝙧𝙐𝙣𝙞𝙩𝙚𝙙 (mute.333)
2025-08-23 22:36:59 xấu hổ dần đi là vừa cái loại ko lm vẫn cs ăn CÁC BẠN ĐỌC CHAT CỦA MIK VS CÔ HOÀI FAKE VÀ RÚT KINH NGHIỆM Ạ



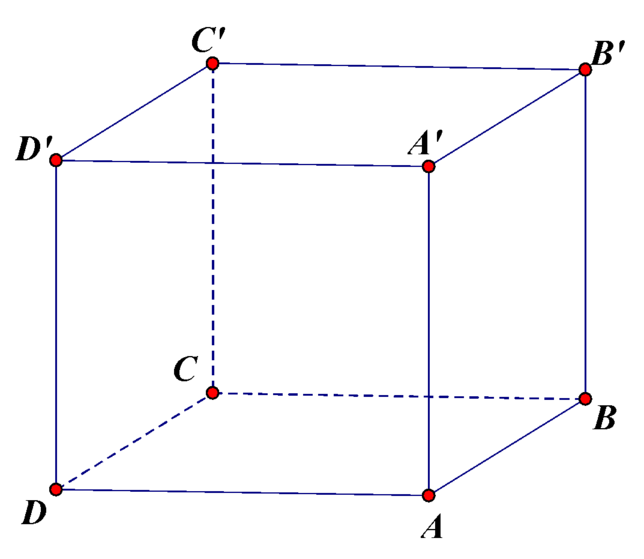
![]() và
và ![]() ,
, ![]() và
và ![]() (
(![]() ).
).![]()
![]()
![]() .
.![]()
![]() .
.![]() với
với ![]() .
.![]()
![]() .
.![]()
![]() .
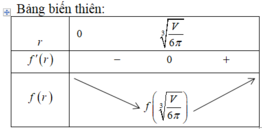
.![]() nhỏ nhất là
nhỏ nhất là ![]() khi
khi ![]() .
.![]() hay
hay ![]() triệu đồng.
triệu đồng.