Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A.
• Ta tìm số cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn.
Có 3 trường hợp :
• 7 cuốn còn lại gồm 2 môn toán lý : có C 9 7 cách
• 7 cuốn còn lại gồm 2 môn lý hóa : có C 11 7 cách
• 7 cuốn còn lại gồm 2 môn toán hóa : có C 10 7 cách
Suy ra có C 9 7 + C 11 7 + C 10 7 = 486 cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn. Do đó số cách chọn 8 cuốn sao cho 7 cuốn còn lại có đủ 3 môn là C 15 7 − 486 = 5949 cách.
Xác suất cần tìm là P = 5949 C 15 7 = 661 715 .

Gọi x là số trang của quyển sách
Số trang sách ngày thứ nhất đọc là \(\frac{1}{3}x\)
Số trang sách ngày thứ hai đọc là \(\frac{5}{8}\left(x-\frac{x}{3}\right)=\frac{5x}{12}\)
Theo đề bài ta có phương trình:
\(x-\frac{x}{3}-\frac{5x}{12}=90\)
<=> 12x-4x-5x=1080
<=> 3x=1080
<=> x=360(trang)
Vậy quyển sách có 360 trang

Đổi : 40% = \(\frac{40}{100}=\frac{2}{5}\)
Phân số chỉ số phần số cuốn sách Nam đọc trong ngày cuối cùng là :
1 - \(\frac{2}{7}\)-\(\frac{2}{5}\)= \(\frac{11}{35}\)( cuốn sách )
Quyển sách dày số trang là :
33 : \(\frac{11}{35}\)= 105 ( trang )
Đáp số : 105 trang
phân số chỉ 33 trang còn lại là :
1 ‐ ﴾2/7 +40%﴿ = 11/35 ﴾ tổng số trang sách﴿
quyển sách này dày số trang là
33 :11/35 = 105 ﴾trang﴿
đáp số : 105 trang

Chọn A
Giả sử có a học sinh nhận sách Toán và Lí, b học sinh nhận sách Lí và Hóa, c học sinh nhận sách Toán và Hóa.
Suy ra
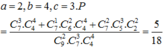

Đáp án B
Số cách chọn 3 cuốn sách trong 10 cuốn để phát ngẫu nhiên cho 3 bạn là: A 10 3

Đáp án B
Số cách chọn 3 cuốn sách trong 10 cuốn để phát ngẫu nhiên cho 3 bạn là: A 10 3 .

Số trang sách ngày thứ nhất Kiên đọc được là:
60 . \(\frac{1}{3}\)= 20 (trang)
Số trang sách còn lại sau ngày thứ nhất đọc là:
60 - 20 =40 (trang)
Số trang sách ngày thứ hai Kiên đọc được là:
40 . \(\frac{3}{5}\) =24 (trang)
Số trang sách ngày thứ ba Kiên đọc được là:
40 - 24=16 (trang)
Đáp số: 16 trang.
Số trang ngày thứ nhất Kiên đọc là:
1 phần 3 nhân 60=20(trang)
Số trang còn lại là:
60-20=40(trang)
Số trang ngày thứ 2 đọc là:
3 phần 5 nhân 40=24(trang)
Số trang ngày thứ ba Kiên đọc là :
60-20-24=16 (trang)
đáp số :16 trang


Đáp án D.
Sô cách lấy bằng số cách chọn ra 6 quyển để bỏ lại. Yêu cầu đặt ra là 6 quyển để lại phải đủ cả 3 môn.
TH1: 1 văn, 2 âm nhạc, 3 hội họa: C 5 1 . C 4 2 . C 3 3 .
TH2: 1 văn, 3 âm nhạc, 2 hội họa: C 5 1 . C 4 3 . C 3 2 .
TH3: 1 văn, 4 âm nhạc, 1 hội họa: C 5 1 . C 4 4 . C 3 1
TH4: 2 văn, 1 âm nhạc, 3 hội họa: C 5 2 . C 4 1 . C 3 3 .
TH5: 2 văn, 2 âm nhạc, 2 hội họa: C 5 2 . C 4 2 . C 3 2 .
TH6: 2 văn, 3 âm nhạc, 1 hội họa: C 5 2 . C 4 3 . C 3 1 .
TH7: 3 văn, 1 âm nhạc, 2 hội họa: C 5 3 . C 4 1 . C 3 2 .
TH8: 3 văn, 2 âm nhạc, 1 hội họa: C 5 3 . C 4 2 . C 3 1 .
TH9: 4 văn, 1 âm nhạc, 1 hội họa: C 5 4 . C 4 1 . C 3 1 .
Lấy 6 quyển sách chia cho 6 bạn: 6 ! = 720
Nhân lại ta có : 579600 cách