Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 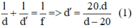
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
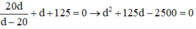
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
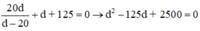
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm

Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 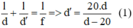
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 45cm
∗ Trường hợp 1
d’ + d = -45cm (2)
Từ (1) và (2) ta có:
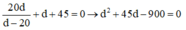
Giải phương trình lấy nghiệm d > 0 ta được: d = 15 cm
∗ Trường hợp 2
d’ + d = 45cm (3)
Từ (1) và (3) ta có:
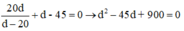
phương trình này vô nghiệm

Khoảng cách vật - ảnh AA' = |d + d'|
a) d + d' = ± 125 ta có:
d1 = 100 cm; d2 = 25 cm; d3 ≈ 17,54 cm.
b) d + d' = ± 45; ta có: d = 15 cm.

a/ \(d=2f=100\Rightarrow A'B'=AB=1\left(cm\right);d'=d=50\left(cm\right)\)
b/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'};-\left(d'+d\right)=45\Rightarrow d'=-45-d\)
\(\Rightarrow\dfrac{1}{50}=\dfrac{1}{d}-\dfrac{1}{45+d}\Leftrightarrow d^2+45d-50.45=0\)
\(\Leftrightarrow\left[{}\begin{matrix}d=30\\d=-75\left(loai\right)\end{matrix}\right.\Rightarrow d=30\left(cm\right)\)
Vậy phải dịch chuyển thấu kính đi một đoạn là 100-30=70 cm, theo chiều lại gần thấu kính

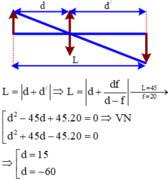
Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính:
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm
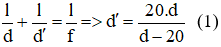
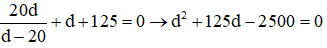
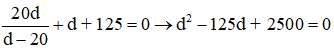

Chọn đáp án D