Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Lực nén vào thanh thép bằng đúng lực đàn hồi xuất hiện trong thanh.
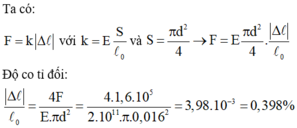

Đáp án: D
Lực nén vào thanh thép bằng đúng lực đàn hồi xuất hiện trong thanh.
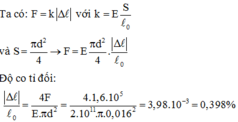

σ = \(\frac{F}{S}=\frac{F}{\frac{d^2.\pi}{4}}=\frac{3450}{\frac{3,14}{4}.\left(5.10^{-2}\right)^2}=17,57.10^5\)
ϵ = \(\frac{\triangle l}{l_0}=\frac{\sigma}{E}=\frac{17,57.10^5}{7.10^{10}}=0,000025\)
Thôi nhá
Đừng tử hỏi tự trả lời nữa
Không ai cạnh tranh đc đâu

d = 20 mm
E = 2.1011 Pa
Fnén = 1,57.105 N
Tìm \(\varepsilon=\dfrac{\left|\Delta t\right|}{l_0}=?\)
Ta có: \(F=k\Delta l=\dfrac{ES}{l_0}\left|\Delta t\right|\)
\(\Rightarrow\dfrac{\Delta l}{l_0}=\dfrac{F}{ES}=25.10^4=0,25.10^{-2}\)
Vậy độ biến dạng tỉ đối của thanh là : \(\dfrac{\left|\Delta l\right|}{l_0}=2,5.10^{-3}\)

Ta có : F = k△l = \(\frac{E.S}{l_0}\). | △l |
→ \(\frac{\triangle l}{l_0}=\frac{F}{E.S}=\frac{157.10^3}{2.10^{11}.\left(10^{-2}\right)^2.3,14}=25.10^{-4}=0,25.10^{-2}\)
Vậy độ biến dạng tỉ đối của thanh là \(\frac{\triangle l}{l_0}=0,25.10^{-2}\)
@phynit
Em trả lời 100% . Không có sự tự hỏi tự trả lời đâu ạ ( Em nói để thầy biết và không nghĩ oan cho em )

Ta có : F = k\(\triangle\)l = \(\frac{E.S}{l_o}\). | \(\triangle\)l |
→ \(\frac{\triangle l}{l_0}=\frac{F}{E.S}=\frac{157.10^3}{2.10^{11}.\left(10^{-2}\right)^2.3,14}\)= 25 . 10-4 = 0,25 .10-2
Vậy độ biến dạng tỉ đối của thanh là \(\frac{\triangle l}{l_0}\)= 0,25 . 10-2

d = 20 mm = 20.10-3m
E = 2.1011 Pa
Fnén = 1,57.105 N
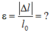
Ta có: 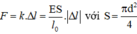
→ Độ biến dạng tỉ đối của thanh:
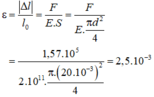

Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)
Đáp án: D
Lực nén vào thanh thép bằng đúng lực đàn hồi xuất hiện trong thanh.
Ta có:
Độ co tỉ đối: