Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

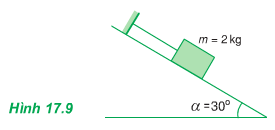
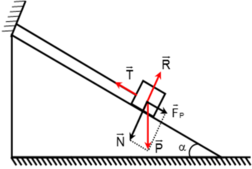
Lực tác dụng lên vật được biểu diễn như hình vẽ:
a) + Khi vật m cân bằng. Ta có:
+
=
+
=
=>
=
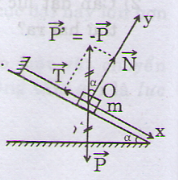
Xét \(\Delta\)P'NO, ta có: sinα = = \(\dfrac{T}{P}\)
=> T = P sin\(\alpha\)
=> T = mg sin30o = 2.9,8. \(\dfrac{1}{2}\) = 9,8 (N)
b) Ta có: cosα = = \(\dfrac{N}{P}\)
=> N = Pcosα = mgcosα = 3. 9,8.
=> N = 16,97N

Hình biểu diễn lực:
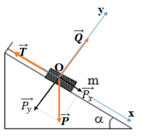
a) Vì vật nằm cân bằng nên ta có:
![]()
Hay
![]()
(ở đây ta phân tích trọng lực P thành 2 lực thành phần Px và Py)
Chiếu (∗) lên trục Ox ta có phương trình về độ lớn sau:
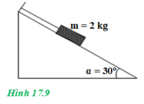
T = Px = P.sin30o = m.g.sin30o = 2. 9,8. 0,5 = 9,8 N.
b) Phản lực của mặt phẳng nghiêng lên vật:
Chiếu (∗) lên trục Oy ta được:
Q – Py = 0 ↔ Q – Pcos30o = 0
→ Q = Py = Pcos30o = 17 (N)

Cơ năng ban đầu: \(W_1=mgh=mg.S.\sin30^0\)
Cơ năng ở chân mặt phẳng nghiêng: \(W_2=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W_1=W_2\)
\(\Rightarrow v=\sqrt{2gS.\sin 30^0}=\sqrt{2.10.10.\sin 30^0}=10(m/s)\)

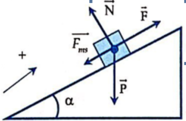
Vật chịu tác dụng của các lực: Lực kéo F → , trọng lực P → , phản lực N → của mặt phẳng nghiêng và lực ma sát F m s → .
Vì ![]() nên vật chuyển động lên theo mặt phẳng nghiêng (được mặc nhiên chọn là chiều dương)
nên vật chuyển động lên theo mặt phẳng nghiêng (được mặc nhiên chọn là chiều dương)
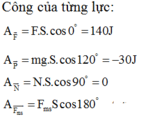
![]()
Tổng công của tất cả các lực tác dụng lên vật là
![]()
![]()

Chọn D.

Vật chịu tác dụng của các lực: Lực kéo F ⇀ , trọng lực P ⇀ , phản lực N ⇀ của mặt phẳng nghiêng và lực ma sát F m s ⇀
Vì P.sinα = 15 N < F = 70 N nên vật chuyển động lên theo mặt phẳng nghiêng (được mặc nhiên chọn là chiều dương).

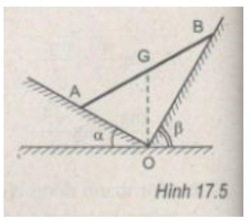
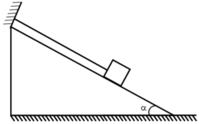
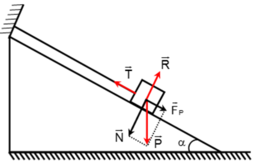
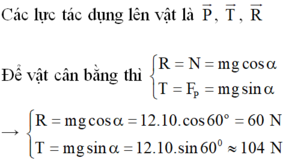
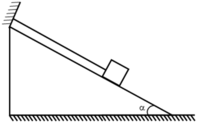

Thanh AB chịu ba lực cân bàng là P → , N 1 → và N 2 → . Vì mặt phẳng nghiêng không ma sát nên hai phản lực N 1 → và N 2 → vuông góc với các mặt phẳng nghiêng. Ta trượt các vectơ lực trên giá của chúng đến điểm đồng quy C (H.17.5G).
Từ tam giác lực, ta được :
N 1 = Psin 30 ° = 20.0,5 = 10 N
N 2 = Pcos 30 ° = 20. 3 /2 = 17,3 ≈ 17 N
Theo định luật III Niu-tơn thì áp lực của thanh lên mặt phẳng nghiêng có độ lớn bằng phản lực của mặt phẳng nghiêng lên thanh.