Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
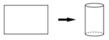
Gọi chiều rộng của hình chữ nhật ban đầu là x(cm), 0<x<18.
⇒ Chiều dài của hình chữ nhật ban đầu là 18-x (cm)
Hình hộp tạo thành có chiều dài là 18-x-6 = 12-x (cm), chiều rộng là x-6 (cm) và chiều cao là 3(cm). Do đó thể tích của hình hộp là


Đáp án là C
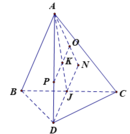
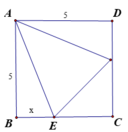
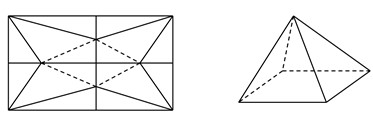
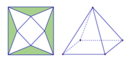
Hình chóp tạo thành có đáy là hình vuông diện tích
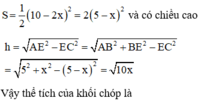


Đáp án D
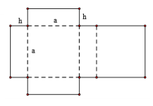
Thể tích khối hộp V = S h = h a 2
Diện tíc của tấm bìa là S b = 4 a h + 2 a 2 = 3 ⇔ h = 3 - 2 a 2 4 a 2
Từ 1 và 2 suy ra V = h a 2 = 3 - 2 a 2 4 a a 2 = a 3 - 2 a 2 4 ≤ 2 4 (khảo sát hàm số)
Dấu “=” xảy ra khi a = 1 2 ⇒ thế vào (2) ta được h = 2 2 ⇒ a + h = 2 .

Đáp án B
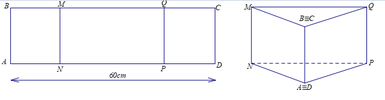
Đặt AN = PD = x suy ra NP = AD-(AN + PD) = 60 - 2x
Gọi H là trung điểm của NP, tam giác ANP cân ⇒ A H ⊥ N P . Suy ra diện tích tam giác ANP là S ∆ A N P = 1 2 . A H . N P = 1 2 . A N 2 - N H 2 . N P = 1 2 A N 2 - N P 2 4 . N P = 1 2 . x 2 - 60 - 2 x 2 4 . 60 - 2 x = 1 2 . 60 x - 900 . 60 - 2 x . . Thể tích khối lăng trụ ANP.BMQ là V = A B . S ∆ A N P = A B . 15 x - 225 . 60 - 2 x . Xét hàm số f x = 30 - x x - 15 trên đoạn [15;30] suy ra m i n [ 15 ; 30 ] f x = 10 5 . Dấu bằng xảy ra khi và chỉ khi x = 20. Vậy độ dài AN = 20 cm.

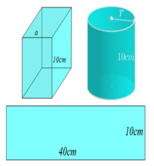
Gọi chiều dài tấm tôn là x (cm) (0 < x < 60) Suy ra chiều rộng: 60 - x (cm)
Giả sử quấn tấm tôn theo cạnh có kích thước x => bán kính đáy r = x 2 π và chiều cao h = 60 - x
Khi đó
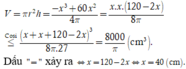
Chọn C.

Đáp án C
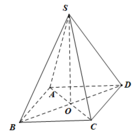
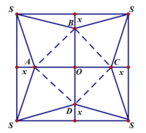
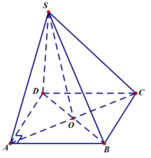
S A = 1 − x 2 2 2 + 1 4 = 1 − x 2 + x 2 2 A O = x 2 2 , S O = S A 2 − A O 2 = 1 − x 2 + x 2 − x 2 2 = 1 − x 2 2 V = 1 3 S O . S A B C D = 1 3 x 2 1 − x 2 2 f ( x ) = x 2 1 − x 2 2 , x ∈ 0 ; 1 f ' ( x ) = 4 x − 5 2 x 2 4 1 − x 2 2 f ' ( x ) = 0 ⇔ x = 0 ( L ) x = 2 2 5

 '
'
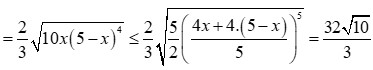
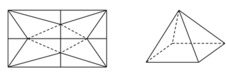
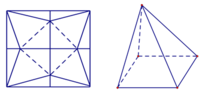
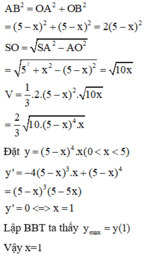
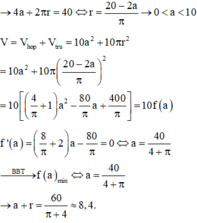
Đáp án B
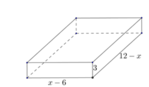
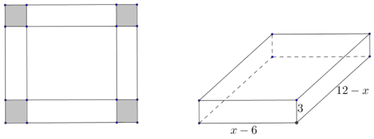
Gọi chiều rộng của hình chữ nhật ban đầu là x (cm), 0 < x < 18
=> Chiều dài của hình chữ nhật ban đầu là 18 - x(cm)
Hình hộp tạo thành có chiều dài là 18 - x - 6 = 12 - x(cm), chiều rộng là x - 6 (cm) và chiều cao là (3cm). Do thể tích của hình hộp là
Từ bảng biến thiên suy ra thể tích lớn nhất