Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Đặt độ dài cạnh AB là x (\(x > 0\))
Theo giả thiết ta có độ dài \(AC = AB + 2 = x + 2\)
Áp dụng định lý pitago trong tam giác vuông ta có
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{x^2} + {{\left( {x + 2} \right)}^2}} = \sqrt {2{x^2} + 4x + 4} \)
b) Chu vi của tam giác là \(C = AB + AC + BC\)
\( \Rightarrow C = x + \left( {x + 2} \right) + \sqrt {2{x^2} + 4x + 4} = 2x + 2 + \sqrt {2{x^2} + 4x + 4} \)
Theo giả thiết ta có
\(\begin{array}{l}C = 24 \Leftrightarrow 2x + 2 + \sqrt {2{x^2} + 4x + 4} = 24\\ \Leftrightarrow \sqrt {2{x^2} + 4x + 4} = 22 - 2x\\ \Rightarrow 2{x^2} + 4x + 4 = {\left( {22 - 2x} \right)^2}\\ \Rightarrow 2{x^2} + 4x + 4 = 4{x^2} - 88x + 484\\ \Rightarrow 2{x^2} - 92x + 480 = 0\end{array}\)
\( \Rightarrow x = 6\) hoặc \(x = 40\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} + 4x + 4} = 22 - 2x\) ta thấy chỉ có \(x = 6\) thỏa mãn phương trình
Vậy độ dài ba cạnh của tam giác là \(AB = 6;AC = 8\) và \(BC = 10\)(cm)

Phương trình x 2 - m x + m 2 - 3 = 0 có hai nghiệm x 1 , x 2 là độ dài các cạnh góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng 2 khi và chỉ khi:
Δ = m 2 − 4 m 2 + 12 ≥ 0 S = x 1 + x 2 = m > 0 P = x 1 . x 2 > 0 x 1 2 + x 2 2 = 4 ⇔ 3 < m ≤ 4 m > 0 x 1 + x 2 2 − 2 x 1 x 2 = 4
⇔ 3 < m ≤ 2 m 2 − 2 m 2 − 3 = 4 ⇔ 3 < m ≤ 2 m 2 = 2 ⇔ m ∈ ∅
Đáp án cần chọn là: D

gọi a, b, c (m) lần lượt là độ dài cạnh huyền, cạnh góc vuông và cạnh góc vuông nhỏ nhất (0<c=<b<a)
theo đề bài ta có: a = b + 2 và b = c + 23
→ a = c + 25
định lý Pythagore:
a2 = b2 + c2 ↔ (c + 25)2 = (c + 23)2 + c2
↔ c2 - 4c - 96 = 0 ↔ c = 12 → a = 37 và b = 35
Vậy độ dài ba cạnh góc vuông lần lượt là 37 (m), 35 (m) và 12 (m)
Gọi a;b;c (m) lần lượt là độ dài cạnh huyên , cạnh góc vuông và cánh góc vuông nhỏ nhất (0<c\(\le\)b<a)
T/C: a=b+2 và b=c+23
\(\rightarrow\)a=c+25
Định lý PYthagore :
a2=b2+c2\(\leftrightarrow\)(c+25)2=(c+23)2+c2
\(\leftrightarrow\)c2-4c-96=0\(\leftrightarrow\)c=12\(\leftrightarrow\)a=37 và b=35
Vậy độ dài cạnh góc vuông lần lượt là:37(m);35(m) và 12(m)

Chọn D.
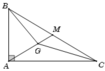
Gọi M là trung điểm của BC
Ta có ![]()
![]()
Mà AM = BC/ 2= 6 nên GA = 2/3. AM = 4

Ta có:
\(\begin{array}{l}5,4\; - 0,2 < a < 5,4\; + 0,2\;\left( {cm} \right);\;\\7,2 - 0,2 < b < 7,2 + 0,2\;\left( {cm} \right);\\9,7 - 0,1 < c < 9,7 + 0,1\;\left( {cm} \right)\end{array}\)
\(\begin{array}{l} \Rightarrow 5,4 + 7,2 + 9,7\; - 0,5 < a + b + c < 5,4 + 7,2 + 9,7\; + 0,5\;\left( {cm} \right)\\ \Leftrightarrow 22,3\; - 0,5 < a + b + c < 22,3 + 0,5\;\left( {cm} \right)\end{array}\)
Vậy chu vi \(P = a + b + c\) của tam giác đó là \(P = 22,3\;cm \pm 0,5\;cm\)
Đặt cạnh huyền của tam giác là x (\(x > 8\))
Theo giải thiết ta tính được cạnh góc vuông là \(x - 8\)
Áp dụng định lý Pitago ta tính được cạnh góc vuông còn lại là \(\sqrt {{x^2} - {{\left( {x - 8} \right)}^2}} = \sqrt {16x - 64} \)
Ta có chu vi của tam giác là \(x + \left( {x - 8} \right) + \sqrt {16x - 64} = 30\)
\(\begin{array}{l} \Leftrightarrow \sqrt {16x - 64} = 38 - 2x\\ \Rightarrow 16x - 64 = {\left( {38 - 2x} \right)^2}\\ \Rightarrow 16x - 64 = 1444 - 152x + 4{x^2}\\ \Rightarrow 4{x^2} - 168x + 1508 = 0\end{array}\)
\( \Rightarrow x = 13\) và \(x = 29\)
Thay \(x = 13\) và \(x = 29\) vào phương trình \(\sqrt {16x - 64} = 38 - 2x\) ta thấy chỉ có \(x = 13\) thảo mãn phương trình
Vậy cạnh huyền có độ dài là 13 cm.