Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài cạnh góc vuông thứ nhất là x(cm)
(Điều kiện: x>0)
Độ dài cạnh huyền là \(x:\frac{20}{29}=\frac{29}{20}x\left(\operatorname{cm}\right)\)
Độ dài cạnh góc vuông thứ hai là:
\(\sqrt{\left(\frac{29}{20}x\right)^2-x^2}=\sqrt{\left(\frac{29}{20}x-x\right)\left(\frac{29}{20}x+x\right)}=\sqrt{\frac{9}{20}x\cdot\frac{49}{20}x}=\frac{21}{20}x\) (cm)
Chu vi tam giác vuông là 210cm nên ta có:
\(x+\frac{29}{20}x+\frac{21}{20}x=210\)
=>3,5x=210
=>x=210:3,5=60(nhận)
vậy: Độ dài cạnh góc vuông thứ nhất là 60cm
Độ dài cạnh góc vuông thứ hai là \(60\cdot\frac{21}{20}=63\left(\operatorname{cm}\right)\)
Độ dài cạnh huyền là \(\frac{29}{20}\cdot60=3\cdot29=87\left(\operatorname{cm}\right)\)

a: Đặt \(\dfrac{AB}{5}=\dfrac{AC}{12}=k\)
=>AB=5k; AC=12k
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(25k^2+144k^2=26^2\)
=>\(k^2=4\)
=>k=2
=>AB=10cm; AC=24cm
b: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-70^0=290^0\)
=>\(2\cdot\left(\widehat{ODC}+\widehat{OCD}\right)=290^0\)
=>\(\widehat{OCD}+\widehat{ODC}=145^0\)
Xét ΔOCD có \(\widehat{COD}+\widehat{OCD}+\widehat{ODC}=180^0\)
=>\(\widehat{COD}=180^0-145^0=35^0\)

Bài 8: Vì em nhắn tin nhờ cô giảng bài 8 nên cô chỉ giảng bài 8 thôi nhé
Gọi các cạnh góc vuông, cạnh huyền của tam giác cần tìm lần lượt là: a; b; c
Theo bài ra ta có: a+b+c =36; \(\dfrac{a}{b}\) = \(\dfrac{3}{4}\)
\(\dfrac{a}{b}\) = \(\dfrac{3}{4}\) ⇒ \(\dfrac{a}{3}\) = \(\dfrac{b}{4}\) ⇒ \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{a^2+b^2}{9+16}\) (1)
Vì tam giác vuông nên ta theo pytago ta có: a2 + b2 = c2 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{c^2}{25}\)
⇒ \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) = \(\dfrac{a+b+c}{3+4+5}\) = \(\dfrac{36}{12}\) = 3
a = 3.3 = 9 (cm)
b = 3.4 = 12 (cm)
c = 3.5 = 15 (cm)
Kết luận: độ dài cạnh bé của góc vuông là: 9 cm
dộ dài cạnh lớn của góc vuông là 12 cm
độ dài cạnh huyền là 15 cm

Bài 9:
a,Gọi độ dài cạnh góc vuông là: a
Theo pytago ta có: a2 + a2 = 22 = 4 ⇒ 2a2 = 4 ⇒ a2 = 2 ⇒ a = \(\sqrt{2}\)
b, Gọi độ dài cạnh góc vuông là :b
Theo pytago ta có:
b2 + b2 = 102 =100 ⇒ 2b2 = 100 ⇒ b2 = 50⇒ b = 5\(\sqrt{2}\)
Bài 8 cô làm rồi nhé.
Bài 10 ; Gọi độ dài các cạnh góc của tam giác vuông lần lượt là:
a; b theo bài ra ta có:
\(\dfrac{a}{5}\) = \(\dfrac{b}{12}\) \(\Rightarrow\) \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{a^2+b^2}{25+144}\) (1)
Theo pytago ta có: a2 + b2 = 522 = 2704 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{2704}{169}\) = 16
⇒ a2 = 25.16 = (4.5)2 ⇒ a = 20
b2 = 144.16 = (12.4)2 ⇒ b = 48

cạnh góc vuông lớn 7.5
cạnh huyền \(\frac{3}{2}\sqrt{41}\)
hình chiếu có 1 thôi vì chung đỉnh 900/41 :) số hơi lẻ

Gọi độ dài cạnh góc vuông nhỏ là x (m)(x > 0)
Độ dài cạnh góc vuông lớn là x + 8 (m)
Khi tăng độ dài cạnh góc vuông nhỏ lên 2 lần ta được cạnh có độ dài 2x (m)
Khi giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được cạnh có độ dài 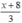 (m)
(m)
Tam giác vuông mới có diện tích bằng 51 m 2
Theo công thức tính diện tích tam giác vuông ta có phương trình:
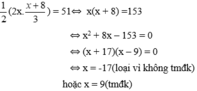
Vậy độ dài cạnh góc vuông nhỏ là 9m. Độ dài cạnh góc vuông lớn là 17m.

Bài giải:
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lí Pitago ta có:
a2 = 72 + 242 = 49 + 576 = 625
Nên a = 25cm
Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có độ dài là 12,5cm.
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lí Pitago ta có:
a2 = 72 + 242 = 49 + 576 = 625
Nên a = 25cm
Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có độ dài là 12,5cm.
Gọi độ dài hai cạnh góc vuông lần lượt là a(m),b(m)(ĐK: a>0;b>0)
Độ dài hai cạnh góc vuông tỉ lệ với 3 và 4 nên \(\dfrac{a}{3}=\dfrac{b}{4}=k\)
=>a=3k; b=4k
Theo đề, ta có: \(a^2+b^2=20^2\)
=>\(25k^2=400\)
=>\(k^2=16\)
=>k=4
=>a=3*4=12; b=4*4=16