Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài của tấm bìa là x (x > 3) (dm)
⇒ Chiều rộng của tấm bìa là x – 3 (dm)
Nếu tăng chiều dài 1 dm và giảm chiều rộng 1 dm thì diện tích là 66 d m 2 nên ta có phương trình:
(x + 1)(x – 3 – 1) = 66
⇔ (x + 1)(x – 4 ) = 66
⇔ x 2 – 3x – 4 – 66 = 0
⇔ x 2 – 3x – 70 = 0
Δ = 3 2 - 4.(-70) = 289 ⇒ ∆ = 17
⇒ Phương trình đã cho có 2 nghiệm
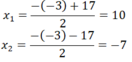
Do x > 3 nên x =10
Vậy chiều dài của tấm bìa là 10 dm
Chiều rộng của tấm bìa là 7 dm.

Đặt chiều rộng là \(x\left(m\right),x>0\).
Khi đó độ dài đường chéo là \(x+10\left(m\right)\).
Áp dụng định lí Pythagore ta có:
\(x^2+20^2=\left(x+10\right)^2=x^2+20x+100\)
\(\Leftrightarrow x=15\)(tm)
Diện tích tấm vải là: \(20\times15=300\left(m^2\right)\)

Gọi chiều dài miếng bìa là
\(x\left(cm;x>4\right)\)
Chiều rộng miếng bìa là:
\(\frac{3x}{5}\left(cm\right)\)
Diện tích ban đầu là:
\(\frac{x\times3}{5}=x^2\times\frac{3}{5}\left(cm^2\right)\)
Diện tích mới của miếng bìa là:
\(\left(x-4\right)\times\left(\frac{3x}{5}-1\right)=\frac{1}{2}\times x^2\times\frac{3}{5}\Leftrightarrow x=10\)
Chu vi miếng bìa đó là:
\(2\times\left(10+\frac{3}{5}\times10\right)=32\left(cm\right)\)
Đáp số: 32 (cm)

Bạn ơi Hình chũ nhật không có đường chéo
Chỉ có hình thoi mới có đường chéo thôi
HỌC TỐT !



Gọi chiều dài của tấm bìa đó là x (x >17) (cm)
Suy ra chiều rộng của tấm bìa là x – 17 (cm)
Áp dụng định lý Py – ta – go, ta có phương trình:
x2 + (x – 17)2 = 532
⇒ x2+ x2 – 34x + 289 – 2809 = 0
⇒ 2x2 – 34 x – 2520 = 0
⇒ x = 45 hoặc x = -28 (loại)
Suy ra chiều rộng của tấm bìa là 28 (cm), Chu vi của tấm bìa các tông là 146 (cm)