Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2\cdot45}{10}}=3s\)
\(L=v_0\cdot t=3v_0\)

Đáp án: D
Chọn gốc tọa độ tại đỉnh tháp, Oy hướng lên. Gốc thời gian là lúc ném vật.
Vận tốc:
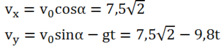
Có:
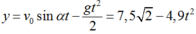
Tại mặt đất thì :
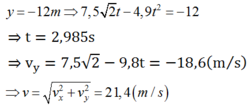

Đáp án D
Chọn gốc tọa độ tại đỉnh tháp, Oy hướng lên. Gốc thời gian là lúc ném vật.
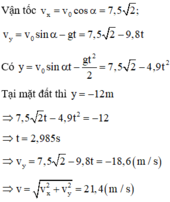

a)Phương trình quỹ đạo của hòn đá:
\(y=\dfrac{g}{2v^2_0}x^2\)
b)Thời gian chuyển động của hòn đá:
\(y=h=\dfrac{1}{2}gt^2\)
\(\Rightarrow t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot25}{10}}=\sqrt{5}\approx2,24s\)
c)Gọi gia tốc toàn phần là \(a=g=10\)m/s2
Gia tốc tiếp tuyến:
\(a_t=\dfrac{g\sqrt{2gh}}{\sqrt{v_0^2+2gh}}=\dfrac{10\sqrt{2\cdot10\cdot25}}{\sqrt{15^2+2\cdot10\cdot25}}=8,3\)m/s2
Gia tốc pháp tuyến:
\(a_n=\sqrt{a^2-a_t^2}=\sqrt{10^2-8,3^2}=5,6\)m/s2
Khoảng cách từ chân tháp đến lúc chạm đất:
\(R=\dfrac{v^2}{a_n}=\dfrac{15^2}{5,6}=40,18\)m

a)Qũy đạo của hòn đá: \(y=25+v_0sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
Thời gian chuyển động của hòn đá:
\(\Rightarrow0=25+v_0\cdot sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
\(\Rightarrow0=25+15\cdot sin30\cdot t-\dfrac{1}{2}\cdot10\cdot t^2\)
\(\Rightarrow t\approx3,11s\)
b)Khoảng cách từ chân tháp đến chỗ rơi:
\(S=x=v_0\cdot cos\alpha\cdot t\)
\(\Rightarrow S=15\cdot sin30\cdot3,11=23,325m\)
c)Ta có: \(v_x=v_0\cdot cos\alpha\)
\(v_y=v_0\cdot sin\alpha-gt\)
Vận tốc hòn đá lúc chạm đất:
\(v=\sqrt{(v_0\cdot sin\alpha)^2+\left(v_0\cdot sin\alpha-gt\right)^2}\)
\(=\sqrt{\left(15\cdot sin30\right)^2+\left(15\cdot sin30-10\cdot3,1\right)^2}\)
\(\approx24,7\)m/s
ở trên cho vx=v0⋅cosα sao xuống dưới chuyển thành sin rồi, v của bài này là 26,94 m/s ấy.

Sau 4 giây, vận tốc của người và đá làv0=at=0,5.4=2(m/s)v0=at=0,5.4=2(m/s)Độ cao của hòn đá lày=0,5at2=4(m)y=0,5at2=4(m)Chuyển động của hòn đá sau khi ném là 1 chuyển động ném ngangTa áp dụng công thức của chuyển động ném ngangy=0,5at2+v0yt+y0⇔−0,5.10t2+(2+5,4.sin300)t+4=0⇒t=1,48(s)y=0,5at2+v0yt+y0⇔−0,5.10t2+(2+5,4.sin300)t+4=0⇒t=1,48(s)x=v0x.t
Hop voi betong 1 goc =?