Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
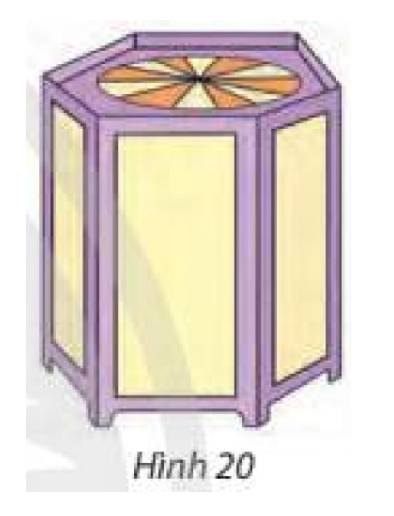
Diện tích một mặt bên của lồng đèn là: \(10.30 = 300\left( {c{m^2}} \right)\)
Tổng diện tích các mặt bên của chiếc lồng đèn đó là: \(300.6 = 1800\left( {c{m^2}} \right)\)
a) Tam giác đều ABC có diện tích \(S = \frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Tam giác đều A'B'C' có diện tích \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích khối chóp cụt
\(V = \frac{1}{3}.HH'.\left( {S + S' + \sqrt {S.S'} } \right) = \frac{1}{3}.h.\left( {{a^2}\sqrt 3 + \frac{{{a^2}\sqrt 3 }}{4} + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} } \right) = \frac{{7{a^2}\sqrt 3 }}{{12}}\)
b) Vì ABC.A'B'C' là khối chóp cụt đều nên (ABC) // (A'B'C')
Mà \(\left( {A{B_1}{C_1}} \right) \subset \left( {ABC} \right) \Rightarrow \left( {A{B_1}{C_1}} \right)//\left( {A'B'C'} \right)\)
Xét tam giác ABC có
B1,C1 tương ứng là trung điểm của AB, AC
\( \Rightarrow \) B1C1 là đường trung bình của tam giác ABC
\( \Rightarrow \) \({B_1}{C_1} = \frac{{BC}}{2}\) và B1C1 // BC mà \(B'C' = \frac{{BC}}{2}\) và BC // B’C’
\( \Rightarrow \) B1C1 = B’C’ và B1C1 // B’C’ \( \Rightarrow \) C1C’B’B1 là hình bình hành
Ta có \(A{B_1} = A'B' = \frac{{AB}}{2},A{B_1}//A'B'\) \( \Rightarrow \) AA’B’B1 là hình bình hành.
\(A{C_1} = A'C' = \frac{{AC}}{2},A{C_1}//A'C'\) \( \Rightarrow \) AA’C’C1 là hình bình hành.
Do đó AB1C1.A'B'C' là một hình lăng trụ
Thể tích hình lăng trụ \(V = HH'.S' = h.\frac{{{a^2}\sqrt 3 }}{4}\)
a)
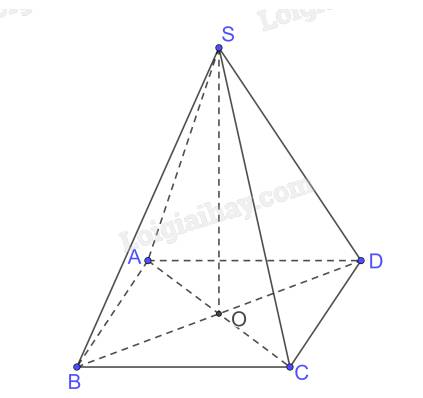
Gọi \(AC \cap BD = \left\{ O \right\}\) mà S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)
\( \Rightarrow \) O là hình chiếu của S trên (ABCD)
C là hình chiếu của C trên (ABCD)
\( \Rightarrow \) OC là hình chiếu của SC trên (ABCD)
\( \Rightarrow \) (SC, (ABCD)) = (SC, OC) \( = \widehat {SCO}\)
Mà cạnh bên tạo với mặt đáy một góc bằng \({60^0}.\)
\( \Rightarrow \widehat {SCO} = {60^0}\)
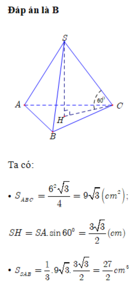
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{6^2} + {6^2}} = 6\sqrt 2 \left( {cm} \right)\)
\( \Rightarrow OC = \frac{{AC}}{2} = \frac{{6\sqrt 2 }}{2} = 3\sqrt 2 \left( {cm} \right)\)
Xét tam giác SOC vuông tại O có
\(\tan \widehat {SCO} = \frac{{SO}}{{OC}} \Rightarrow SO = 6\sqrt 2 .\tan {60^0} = 6\sqrt 6 \left( {cm} \right)\)
\({S_{ABCD}} = {6^2} = 36\left( {c{m^2}} \right)\)
Vậy khối chóp có thể tích \(V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.6\sqrt 6 .36 = 72\sqrt 6 \left( {c{m^3}} \right)\)
b)
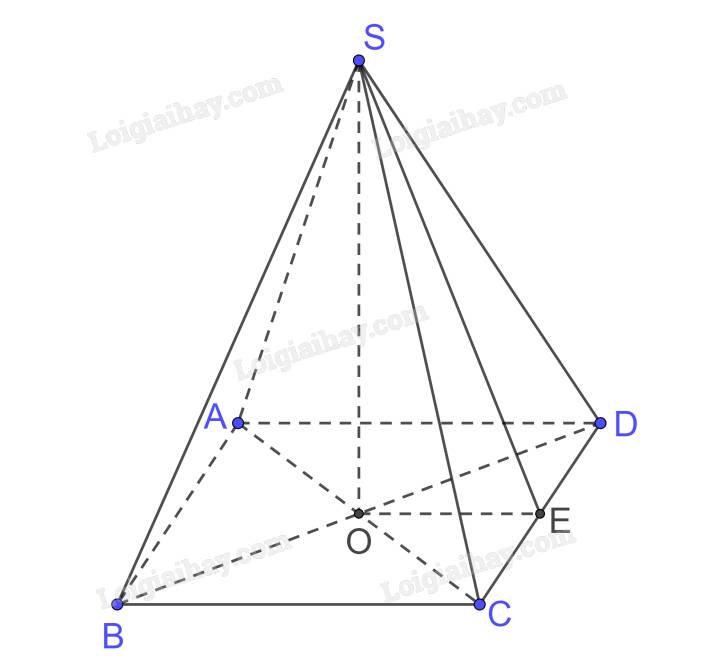
Trong (ABCD) kẻ \(OE \bot CD\)
\(\begin{array}{l}SO \bot CD\left( {SO \bot \left( {ABCD} \right)} \right)\\ \Rightarrow CD \bot \left( {SOE} \right),SE \subset \left( {SOE} \right) \Rightarrow CD \bot SE,OE \bot CD,\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\ \Rightarrow \left( {\left( {SCD} \right),\left( {ABCD} \right)} \right) = \left( {SE,OE} \right) = \widehat {SEO}\end{array}\)
Mà mặt bên tạo với mặt đáy một góc bằng \({45^0}.\)
\( \Rightarrow \widehat {SEO} = {45^0}\)
Ta có \(\left. \begin{array}{l}OE \bot CD\\AD \bot CD\end{array} \right\} \Rightarrow OE//AD\) mà O là trung điểm AC nên OE là đường trung bình tam giác ACD.
\( \Rightarrow OE = \frac{{AD}}{2} = \frac{6}{2} = 3\left( {cm} \right)\)
Xét tam giác SOE vuông tại O có
\(\tan \widehat {SEO} = \frac{{SO}}{{OE}} \Rightarrow SO = 3.\tan {45^0} = 3\left( {cm} \right)\)
Vậy khối chóp có thể tích \(V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.3.36 = 36\left( {c{m^3}} \right)\)
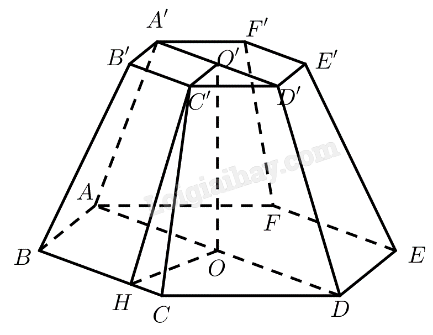
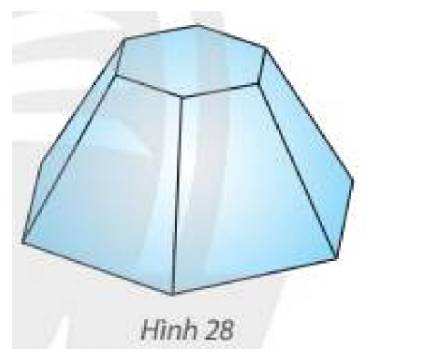
Mô hình hoá hình ảnh cái bục bằng hình chóp cụt lục giác đều \(ABC{\rm{DEF}}{\rm{.}}A'B'C'{\rm{D'E'F'}}\) có \(O\) và \(O'\) là tâm của hai đáy. Kẻ \(C'H \bot BC\left( {H \in BC} \right)\).
Ta có: \(BC = 1;CC' = B'C' = 0,7\).
Diện tích đáy lớn là: \(6.\frac{{B{C^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{2}\)
Diện tích đáy nhỏ là: \(6.\frac{{B'C{'^2}\sqrt 3 }}{4} = \frac{{147\sqrt 3 }}{{200}}\)
\(BCC'B'\) là hình thang cân nên \(HC = \frac{{BC - B'C'}}{2} = 0,15\)
Tam giác \(CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \frac{{\sqrt {187} }}{{20}}\)
Diện tích một mặt bên là: \(\frac{1}{2}\left( {BC + B'C'} \right).C'H = \frac{{17\sqrt {187} }}{{400}}\)
Diện tích sáu mặt bên là: \(6.\frac{{17\sqrt {187} }}{{400}} = \frac{{51\sqrt {187} }}{{200}}\)
Diện tích cần sơn là: \(\frac{{51\sqrt {187} }}{{200}} + \frac{{3\sqrt 3 }}{2} + \frac{{147\sqrt 3 }}{{200}} \approx 7,36\left( {{m^2}} \right)\)
Diện tích đáy lớn là: \(S = A{B^2} = {3^2} = 9\)
Diện tích đáy bé là: \(S' = {2^2} = 4\)
Thể tích hình chóp cụt là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.4\left( {9 + \sqrt {9.4} + 4} \right) = \frac{{76}}{3} \approx 25,3\left( {d{m^3}} \right)\)
Gọi \(O,O'\) lần lượt là tâm của hai đáy \(ABC\) và \(A'B'C'\), \(M,M'\) lần lượt là trung điểm của \(BC\) và \(B'C'\).
Kẻ \(A'H \bot AO\left( {H \in AO} \right) \Rightarrow A'H = OO'\)
\(\Delta ABC\) đều \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
\(\Delta A'B'C'\) đều \( \Rightarrow A'M' = \frac{{\frac{a}{2}.\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4} \Rightarrow A'O' = \frac{2}{3}A'M' = \frac{{a\sqrt 3 }}{6}\)
\(A'HOO'\) là hình chữ nhật \( \Rightarrow OH = A'O' = \frac{{a\sqrt 3 }}{6}\)
\( \Rightarrow AH = AO - OH = \frac{{a\sqrt 3 }}{6}\)
Tam giác \(AA'H\) vuông tại \(H\)
\( \Rightarrow OO' = A'H = \sqrt {AA{'^2} - A{H^2}} = \frac{{a\sqrt {141} }}{6}\)
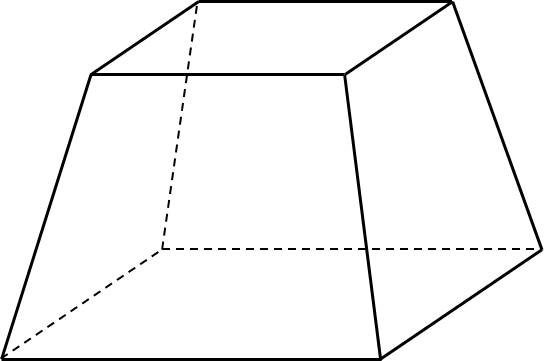
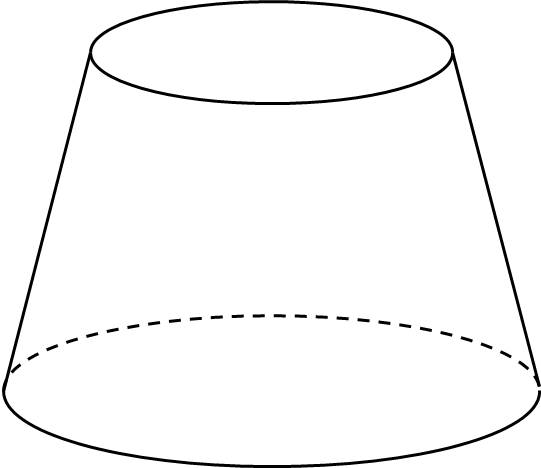
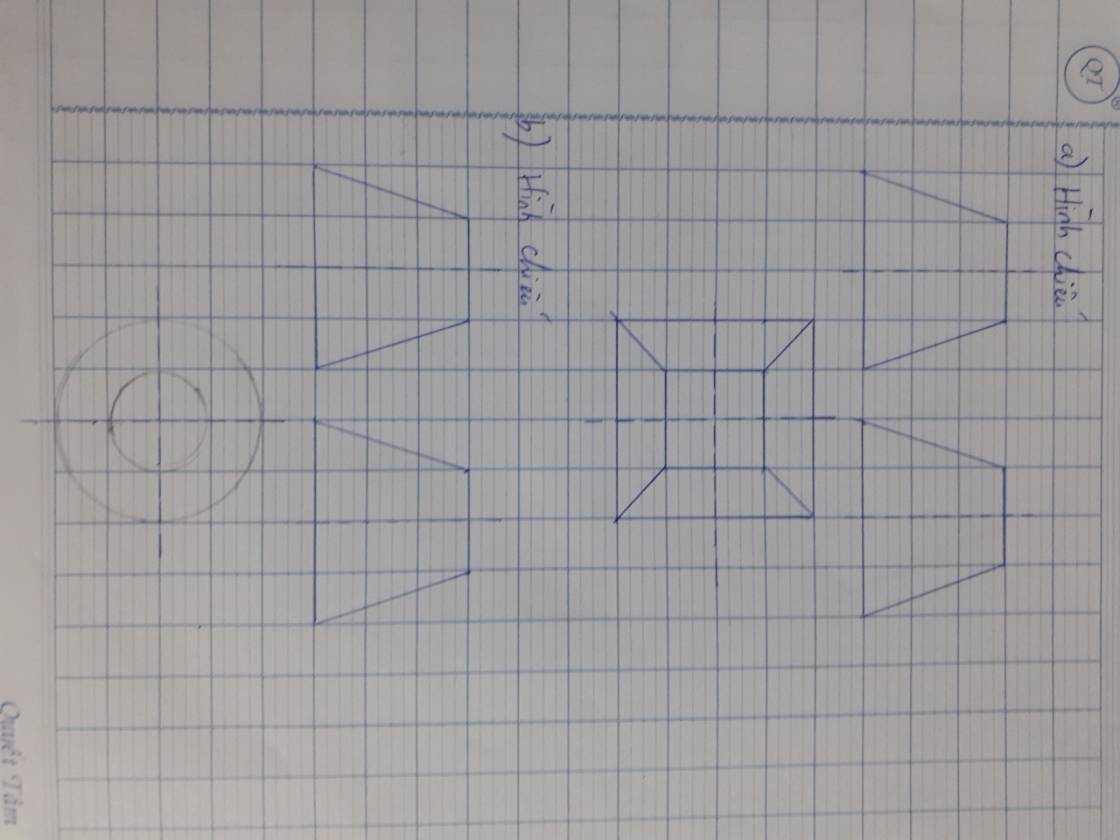
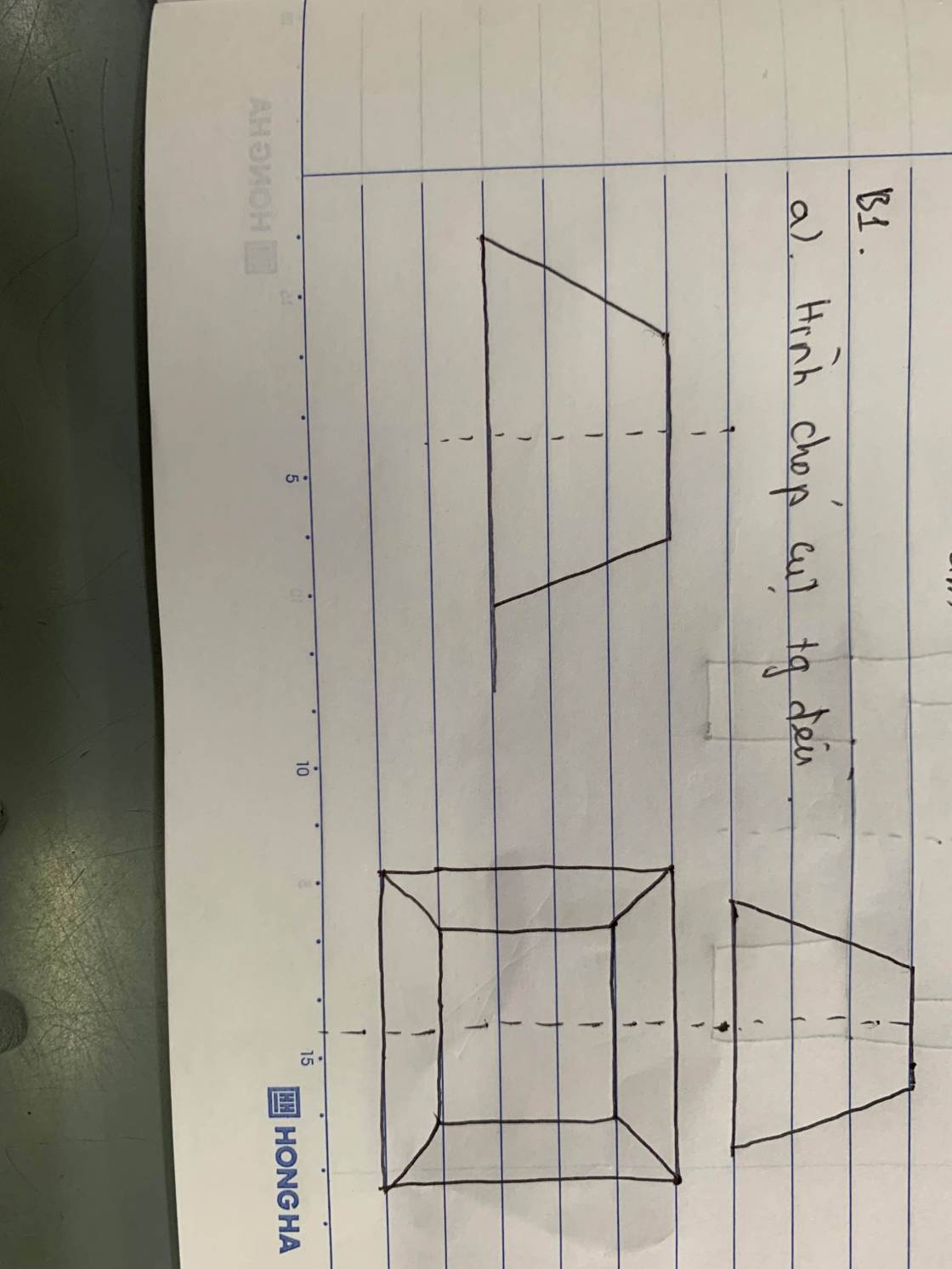
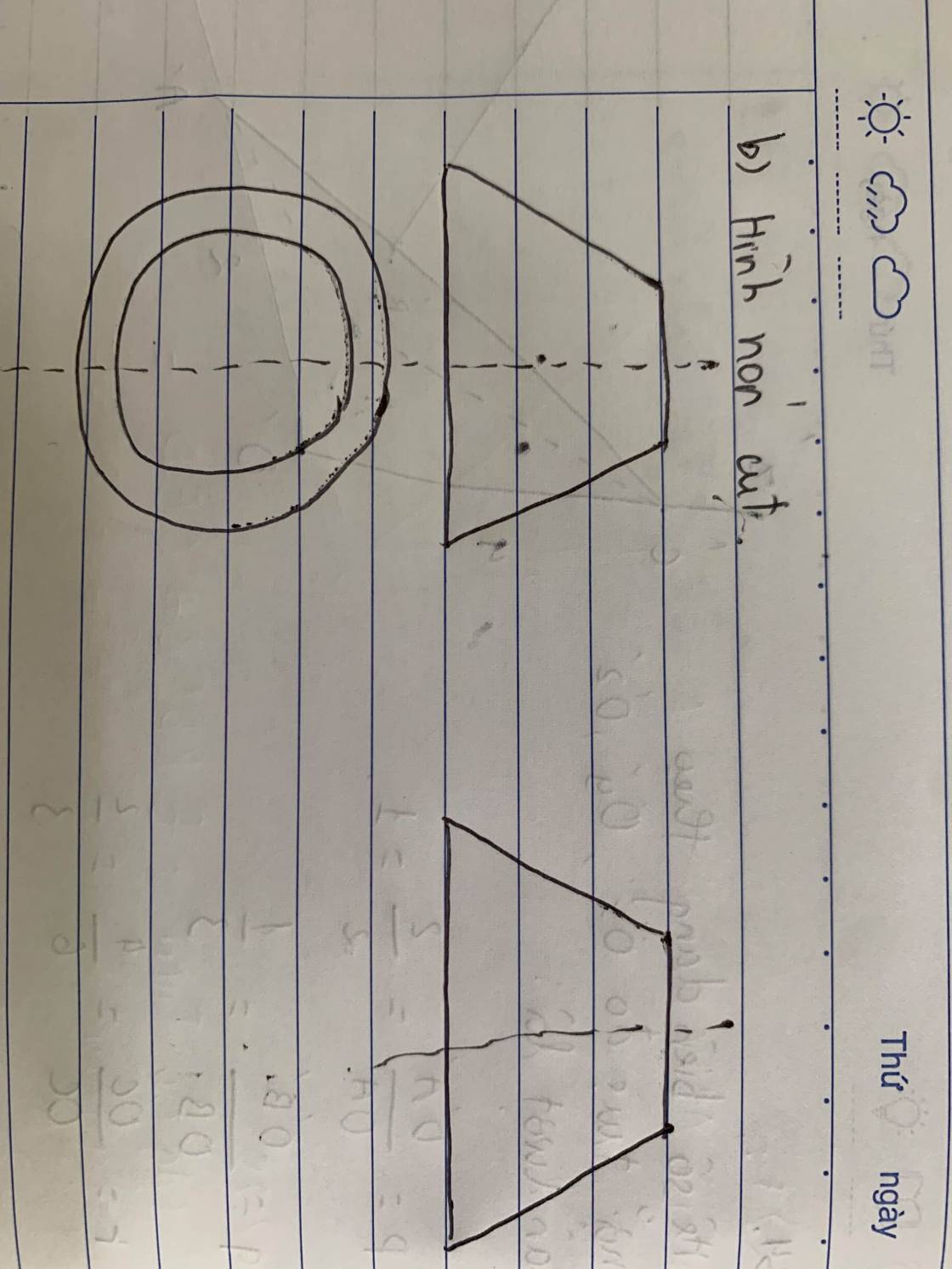
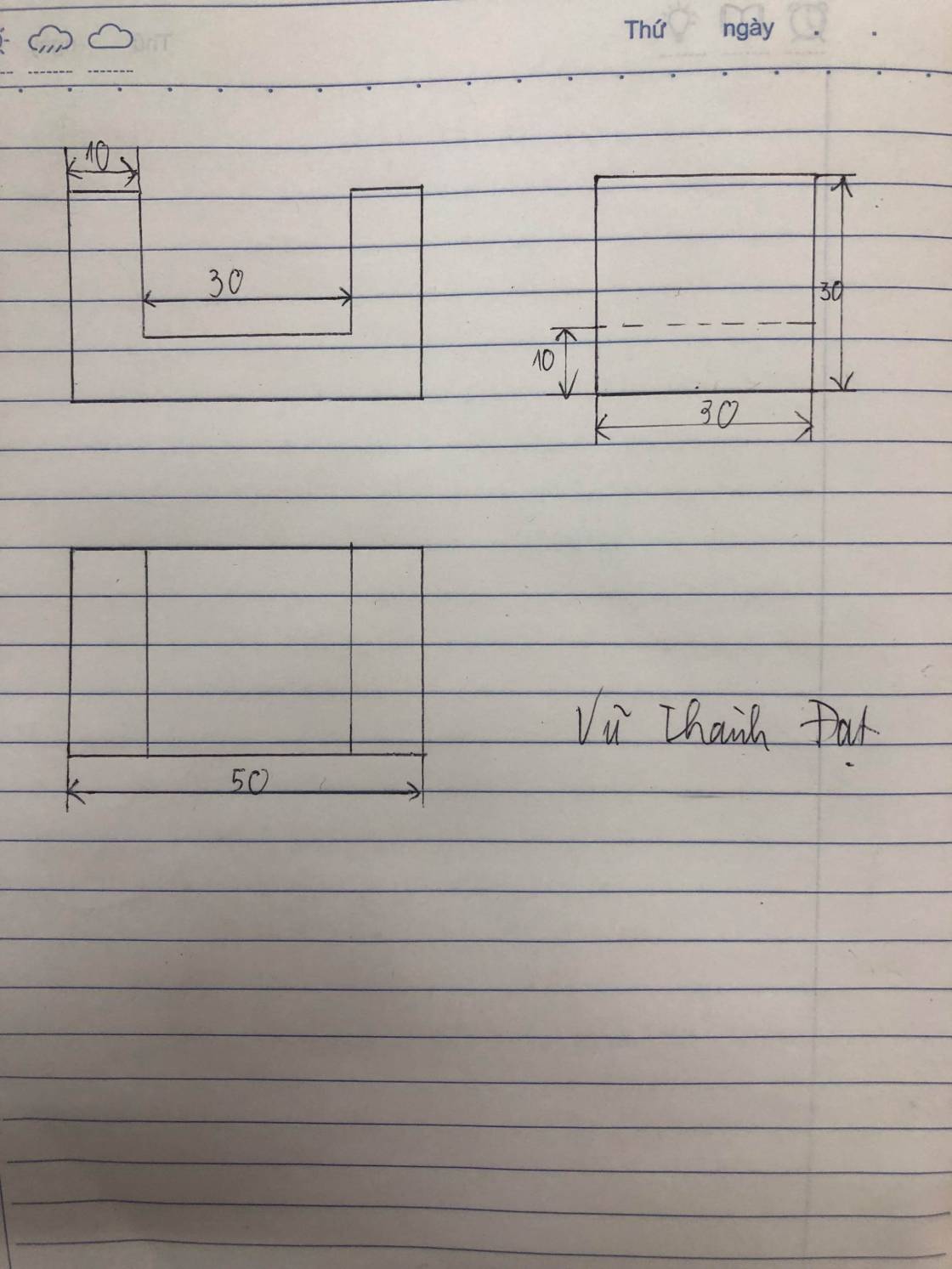
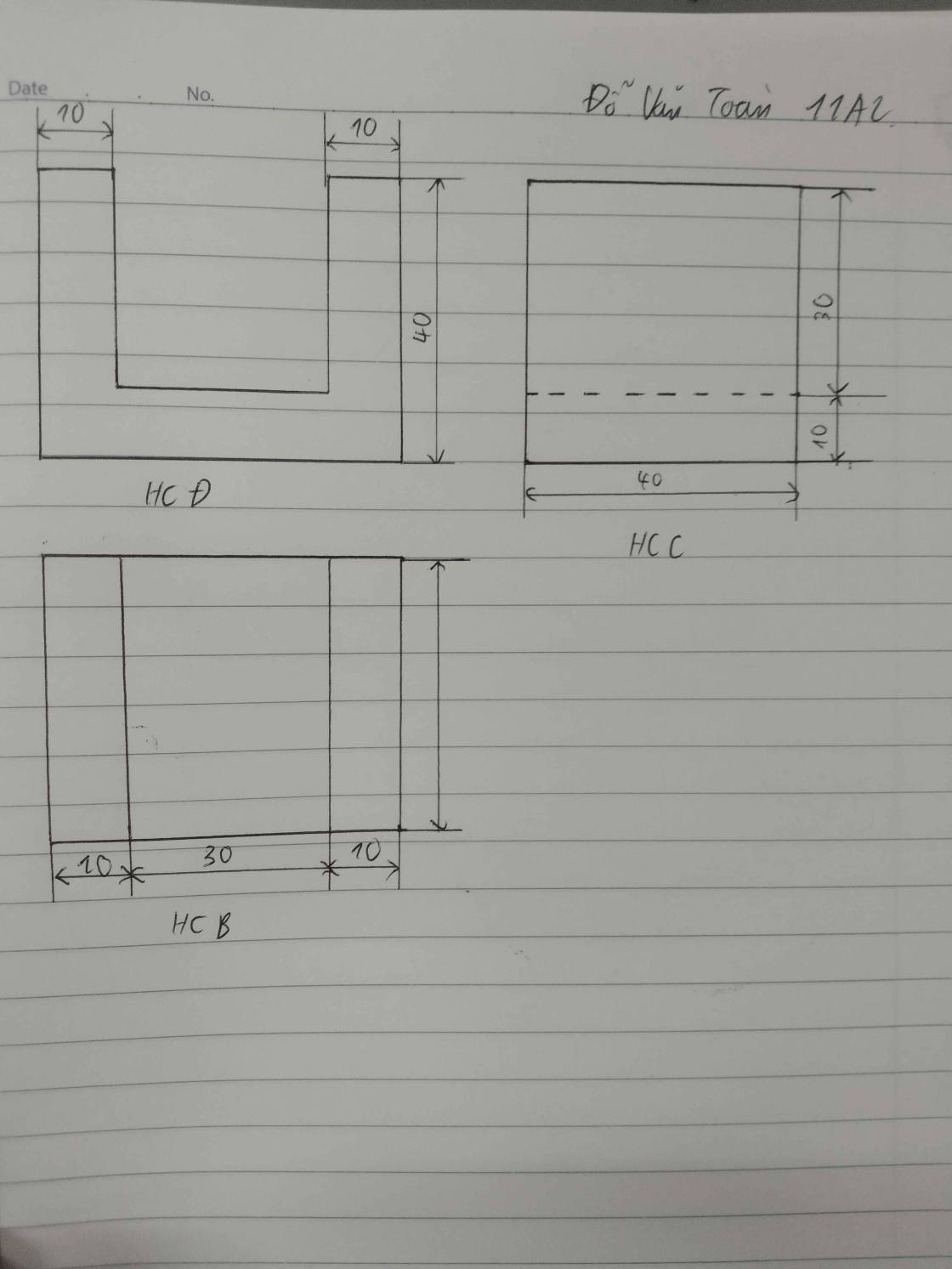
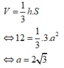
Diện tích đáy lớn là:
\(S_1=60^2=3600\left(cm^2\right)\)
Diện tích đáy nhỏ là;
\(S_2=30^2=900\left(cm^2\right)\)
Chiều cao là:
\(\sqrt{50^2-\dfrac{30^2}{2}}=5\sqrt{82}\left(cm\right)\)
Thể tích là;
\(V=\dfrac{1}{3}\cdot h\cdot\left(S_1+S_2+\sqrt{S_1\cdot S_2}\right)\)
\(=\dfrac{1}{3}\cdot5\sqrt{82}\left(900+3600+\sqrt{900\cdot3600}\right)\)
\(\simeq95082\left(cm^3\right)\)