Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Sóng dừng trên dây có 2 đầu cố định thì tần số cơ bản \(f_0\) (tần số nhỏ nhất để có sóng dừng ứng với 1 bó sóng)
Thì các tần số để có sóng dừng là: \(f_n=n.f_0\)
Suy ra: \(f_0=8Hz\)
Có: \(\dfrac{1}{\lambda_{n+1}}-\dfrac{1}{\lambda_{n}}=\dfrac{f_{n+1}}{v}-\dfrac{f_{n}}{v}=\dfrac{8}{v}=0,2\Rightarrow v=40m/s\)
Tần số âm cơ bản ứng với 1 bó sóng ta có: \(l=\dfrac{\lambda}{2}=\dfrac{v}{2f_0}=\dfrac{40}{2.8}=2,5m\)
Chọn D.

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Từ ĐK đầu bài ta có:
tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:

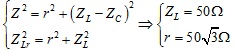
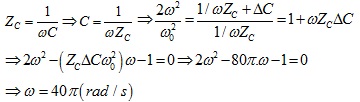
+ Nhìn vào đồ thị ta thấy quãng đường mà sóng truyền được trong thời gian ∆ t = 0,3 s là: s = 3 8 λ → v = s ∆ t = 3 λ 8 . 0 , 3 = 5 λ 4
+ T = λ v = λ . 4 5 λ = 0 , 8 s s.
Đáp án D