Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Theo giả thuyết điểm N dao động nhanh pha hơn điểm M: 2 π 3 (tương ứng λ/3).
Cùng với giả thuyết hai điểm có cùng biên độ, điểm N sớm pha hơn M, vậy ta kết luận pha của hai điểm như hình vẽ.
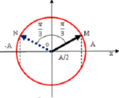
Vậy điểm M có pha π 6 , như hình vẽ. Và biểu thức liên hệ giữa biên độ là:
x = 3 2 A ⇒ A = 2 3 x = 2 3 . 3 = 2 3 c m

Đáp án C
Phương pháp: Phương trình của li độ và vận tốc:
u = Acos ( ωt + φ ) v = ωAcos ( ωt + φ + π 2 )
Cách giải:
Độ lệch pha giữa M và N:
∆ φ = 2 π . MN λ = 2 π . 90 40 = 4 , 5 π
Phương trình li độ và vận tốc tại M và N:
u M = Acos ( ωt + φ ) v M = ωAcos ( ωt + φ + π 2 ) u N = Acos ( ωt + φ + 4 , 5 π ) v N = ωAcos ( ωt + φ + π 2 + 4 , 5 π ) = - ωAcos ( ωt + φ )
Tại thời điểm t thì:
u M = Acos ( ωt + φ ) = 2 cm v N = - ωAcos ( ωt + φ ) = 125 , 6 cm
⇒ v N u M = ω = 125 , 6 2 = 62 , 8 = 2 πf ⇒ f = 10 Hz

Đáp án C
+ Hai điểm M, N dao động vuông pha với nhau, do M gần nguồn sóng hơn nên khi N ở vị trí thấp nhất thì M đã đạt trạng thái thấp nhất trước đó t = T 4 Vậy thời gian ngắn nhất để M chuyển trạng thái như N là t ' = 3 T 4 = 3 4 f = 3 80 s

\(\lambda = v/f=20/50=0.4cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{4,8-5,3}{0,4}-\frac{0}{2\pi})|=|2a\cos\frac{-5\pi}{4}|=\sqrt{2}a = 2\sqrt{2}\)
\( u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})=2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4}+\frac{0}{2}) = 2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4})\\ = 2\sqrt{2}\cos(40 \pi t - 25,25\pi)mm.\)
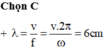
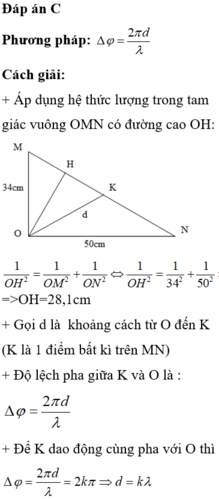



+ Phương trình sóng tại nguồn là u O = A cos ω t − 2 π d λ
→ Đáp án C