

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chu kì: T = 2(s)
Bước sóng: \(\lambda = v.T=80cm.\)
Độ lệch pha giữa M và N là: \(\Delta \varphi = \dfrac{2\pi d}{\lambda}=\dfrac{\pi}{2}\)
Như vậy, M vuông pha với N, và ở thời điểm t2 = (t1+ 1) s, N trễ pha thêm một lượng \(\pi\)
Khi đó, M vẫn vuông pha với N
\(\Rightarrow (\dfrac{3}{5})^2+(\dfrac{u_N}{5})^2=1\)
\(\Rightarrow u_N=\pm4cm\)
Thư Hoàngg Hai dao động vuông pha với nhau thì ta luôn có mối liên hệ như vậy.
Nếu x1 vuông pha với x2 thì:
\((\dfrac{x_1}{A_1})^2+(\dfrac{x_2}{A_2})^2=1\)

Đáp án B
+ Độ lệch pha giữa hai điểm A và B:
∆ φ A B = 2 π ∆ x A B f v = ( 2 k + 1 ) π → v = 4 2 k + 1 m/s
+ Với khoảng giả trị của vận tốc: 0 , 7 m / s ≤ v ≤ 1 m / s → v = 0 , 8 m → λ = 4 cm

Đáp án D
+ Độ lệch pha dao động của hai phần tử A và B
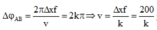 cm/s
cm/s
+ Với khoảng giá trị của tốc độ truyền sóng: 45 c m ≤ v ≤ 60 c m / s
→ Kết hợp với chức năng Mode→7 của Casio ta tìm được v=55 cm/s

Bước sóng: \(\lambda=\frac{v}{f}=\frac{25}{0,5}=50cm\)
Phương trình sóng tại điểm M: \(u_M=3\cos\left(\pi t-\frac{2\pi d}{\lambda}\right)=3\cos\left(\pi t-\frac{2\pi.25}{50}\right)=3\cos\left(\pi t-\pi\right)\)(cm)
Phương trình vận tốc của M: \(v_M=u_M'=-3\pi\sin\left(\pi t-\pi\right)\)(vận tốc bằng đạo hàm bậc nhất của li độ)
Thay t = 2,5s vào PT ta đc: \(v_M=-3\pi\sin\left(\pi.2,5-\pi\right)=3\pi\)(cm/s)
cho mình hỏi vì sao Vm = -3pi(2,5pi - pi) lại bằng 3pi, mình bấm k ra