Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn: Chọn đáp án B
Kinh nghiệm: Bài toán cho v1 thì nên làm theo cách 1.
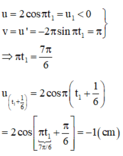

Đáp án A
+ Tốc độ dao động của các phần tử môi trường v max = ωA = 2 π . 3 = 6 π cm / s .
+ Độ lệch pha dao động giữa M và N: ∆ φ = 2 π ∆ x λ = 2 π 7 λ 3 λ = 4 π + 2 π 3 rad .
+ Taị thời điểm t1 điểm M có tốc độ v1 = vmax = 6π cm/s.
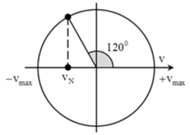
→ Biễu diễn các dao động tương ứng trên đường tròn, ta thu được
v N = 1 2 v max = 1 2 . 6 π = 3 π cm / s .

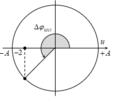
+ Độ lệch pha giữa hai điểm M và O là
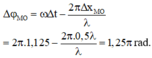
→ Biểu diễn dao động của điểm O và M tương ứng trên đường tròn. Tại thời điểm ban đầu điểm O đang ở vị trí biên dương.
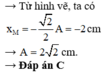

Hướng dẫn: Chọn đáp án B
Cách 1:
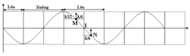
Vẽ đường sin, quy ước sóng truyền theo chiều dương và xác định các vùng mà các phần tử vật chất đang đi lên và đi xuống.
Vì sóng truyền qua M rồi mới đến N nên M nằm bên trái và N nằm bên phải. Mặt khác, vì u M = + 4 c m v à u N = - 4 c m nên chúng phải nằm đúng vị trí như trên hình vẽ (cả M và N đều đang đi lên).
Vì M cách đỉnh gần nhất là p/12 nên thời gian ngắn nhất M đi từ vị trí hiện tại đến vị trí cao nhất là T/12 nên t1 = T/12.
Thời gian ngắn nhất để N đến vị trí cân bằng là T/6 và thời gian ngắn nhất đi từ vị trí cân bằng đến vị trí cao nhất là T/4 nên t2 = T/6 + T/4 = 5T/12 Þ Chọn B.
Cách 2:
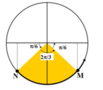
Dao động tại M sớm pha hơn tại N (M quay trước N):

Để M lên đến vị trí cao nhất (M ở biên dương) thì nó phải quay thêm một góc π/6 = ( 1/12 ) .2 π = ( 1/12 ) vòng, tương ứng với thời gian t1 = T/12.
Để N lên đến vị trí cao nhất (N ở biên dương) thì nó phải quay thêm một góc 2π/3+π/6 = ( 5 /12 ) .2 π = ( 5 /12 ) vòng, tương ứng với thời gian t2 = 5T/12. Þ Chọn B.
Chú ý: Xét hai điểm điểm M, I trên cùng một phương truyền sóng cách nhau một khoảng 0 < x < λ / 4.
Nếu ở thời điểm t, điểm I đang ở vị trí cân bằng thì lúc này điểm M cách vị trí cân bằng của nó một đoạn u M = A sin 2 π x λ .
Nếu ở thời điểm t, điểm I đang ở vị trí cao nhất (thấp nhất) thì lúc này điểm M cách vị trí cân bằng của nó một đoạn u M = A cos 2 π x λ .
Ở Câu trên, hiện tại I đang ở vị trí cân bằng nên
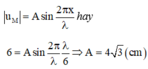

Độ lệch pha của M so với nguồn: \(\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{2\pi\frac{\lambda}{6}}{\lambda}=\frac{\pi}{3}\)rad
(M trễ pha hơn nguồn N)
Biểu diễn trạng thái dao động của M và nguồn trên véc tơ quay như sau:
N (thời điểm t1) N(t1+ T/4) M 60 3 O
Từ giản đồ véc tơ ta dễ dàng suy ra biên độ: A = 3.2 = 6cm.

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)


chịu
tại t1 vật ở vị trí \(-\frac{\pi}{6}\)
sau 1/6s => góc quét \(\Delta\varphi=\frac{\pi}{6}\) => x=0