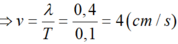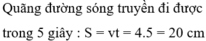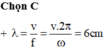Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
@ Lời giải:
+ Chu kỳ 1à khoảng thời gian sóng truyền đi đuợc quãng đuờng bằng 1 buớc sóng .

Dựa vào phương trình sóng => \(\lambda = 2 \pi (m), f = 50Hz\)
Tốc độ truyền sóng là \(v = \lambda.f=2\pi50= 100\pi (m/s)\)
Tốc độ cực đại của phần tử vật chất môi trường là \(v_{max}= A.w=3.100\pi (m/s)\)
\(\Rightarrow \frac{v}{v_{max}} = \frac{100\pi}{3.100\pi}=\frac{1}{3} \)

Đáp án A
Phương pháp: Đồng nhất với phương trình sóng dừng và áp dụng công thức tốc độ truyền sóng v = λ T
Cách giải:
Ta có: 2 π x λ = π x 4 ω = 20 π ⇒ v = λ T = 80 c m / s

Đáp án B
Từ phương trình truyền sóng, ta có: ω = 20 π 2 π λ = 5 π → T = 0 , 1 λ = 0 , 4
Trong mỗi chu kì sóng truyền đi được một quãng đường bằng bước sóng → trong khoảng thời gian ∆ t = 5 T = 5 s sóng truyền đi được S = 50 λ = 20cm.

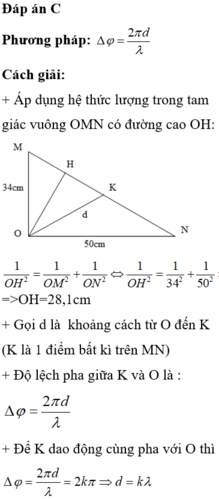
Đáp án C
Phương pháp: Phương trình của li độ và vận tốc:
u = Acos ( ωt + φ ) v = ωAcos ( ωt + φ + π 2 )
Cách giải:
Độ lệch pha giữa M và N:
∆ φ = 2 π . MN λ = 2 π . 90 40 = 4 , 5 π
Phương trình li độ và vận tốc tại M và N:
u M = Acos ( ωt + φ ) v M = ωAcos ( ωt + φ + π 2 ) u N = Acos ( ωt + φ + 4 , 5 π ) v N = ωAcos ( ωt + φ + π 2 + 4 , 5 π ) = - ωAcos ( ωt + φ )
Tại thời điểm t thì:
u M = Acos ( ωt + φ ) = 2 cm v N = - ωAcos ( ωt + φ ) = 125 , 6 cm
⇒ v N u M = ω = 125 , 6 2 = 62 , 8 = 2 πf ⇒ f = 10 Hz