Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Gọi độ dài cạnh của hình vuông là x (m) thì độ dài cạnh tam giác đều là 2x (m).
Chiều dài phần dây được uống thành hình vuông (chính là chu vi hình vuông) là 4x (m); chiều dài phần dây được uốn thành tam giác đều (chính là chu vi hình tam giác đều) là 6x(m) .
Suy ra chiều dài phần dây được uốn thành hình tròn là L - 4 x - 6 x = L - 10 x ( m )
Từ đó ta có x ∈ 0 ; L 10
Gọi r là bán kính của đường tròn thì chu vi đường tròn là
![]()
Tổng diện tích của ba hình là
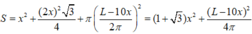
Xét hàm số
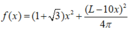
trên 0 ; L 10
Ta có

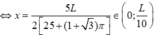
Lập bảng biến thiên ta thấy
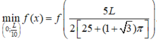
Vậy tổng diện tích của ba hình thu được nhỏ nhất khi x = 5 L 2 25 + 1 + 3 π
suy ra độ dài cạnh của tam giác đều là 2 x = 5 L 25 + 1 + 3 π

Đáp án A
Gọi độ dài các sợi dây uốn thành hình vuông và hình tròn lần lượt là x , y ⇒ x + y = 60 và x,y chính là chu vi của các hình trên.
Diện tích hình vuông là S 1 = x 4 2 = x 2 16 ; Diện tích hình tròn là S 2 = π y 2 π 2 = y 2 4 π
Tổng diện tích hai hình
S = S 1 + S 2 = x 2 16 + y 2 4 π ⇒ S . 16 + 4 π = x 2 16 + y 2 4 π 16 + 4 π ≥ x + y 2 = 3600 ⇒ S ≥ 900 4 + π
Đạt được khi
x 16 = y 4 π = x + y 16 + 4 π = 60 16 + 4 π = 15 4 + π ⇒ x = 15.16 4 + π = 33,61

Đáp án C
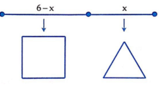
Cắt sợi dây 6 mét đã cho thành hai phần có độ dài lần luột là x mét và 6-x mét 0 < x < 6 . Phần thứ nhất có độ dài x mét được uốn thành hình tam giác đều cạnh bằng x 3 mét. Phần thứ hai có độ dài 6-x mét được uốn thành hình vuông cạnh bằng 6 − x 4 mét.
Diện tích phần I là S 1 = x 3 2 . 3 4 = x 2 3 36 m 2 .
Diện tích phần II là S 2 = 6 − x 4 2 m 2 .
Tổng diện tích hai phần là S x = S 1 + S 2 = x 2 3 36 + 6 − x 4 2 m 2 với x ∈ 0 ; 6
Đạo hàm S ' x = x 3 18 − 6 − x 8 ; S ' x = 0 ⇔ x = 54 9 + 4 3 ∈ 0 ; 6 . Lập bảng biến thiên của hàm số S x trên khoảng 0 ; 6 , ta thấy min S x = S 54 9 + 4 3 .
Khi đó cạnh của tam giác đều bằng 18 9 + 4 3 m .

Tổng đáy lớn và đáy bé là :
360.2 : 12 = 60 ( m )
Tổng số phần bằng nhau là :
2 + 3 = 5 ( phần )
Giá trị một phần là :
60 : 5 = 12 ( m )
Đáy bé là :
12.2 = 24 ( m )
Đáy lớn là :
12.3 = 36 ( m )
Đáp số : Đáy bé : 24 m
Đáy lớn : 36 m

a﴿ Chu vi:
2/5 x 4 = 8/5 ﴾m﴿
Diện tích:
2/5 x 2/5 = 4/25 ﴾m2 ﴿
b﴿ Diện tích 1 ô vuông nhỏ là:
2/25 x 2/25 = 4/625 ﴾m2 ﴿
Số ô vuông cắt được là:
4/25 : 4/625 = 25 ﴾ô vuông﴿
c﴿ Chiều rộng tờ giấy hình chữ nhật là:
4/25 : 4/5 = 1/5 ﴾m﴿

Đáp án là D.
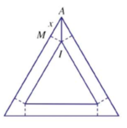
M I = x 3 3 ; S t g = a − 2 x 2 3 4 .
V l t = M I . S t g = a 2 x − 4 a x 2 + 4 x 3 4 ; 0 < x < a 2 .
xét hàm số
f x = 4 x 3 − 4 a x 2 + a 2 x ⇒ f ' x = 12 x 2 − 8 a x + a 2 , cho f ' x = 0 ⇔ x = a 6 x = a 2 l o a i
Thể tích đạt GTLN khi x = a 6 .


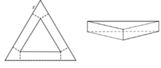
Từ giả thiết suy ra x + y = 10
Diện tích hình chữ nhật là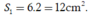
Diện tích tam giác là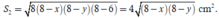
Yêu cầu bài toán: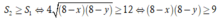
Suy ra y = 5
Vậy có duy nhất một bộ số (x;y) = (5;5) thỏa mãn
Chọn B.