
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
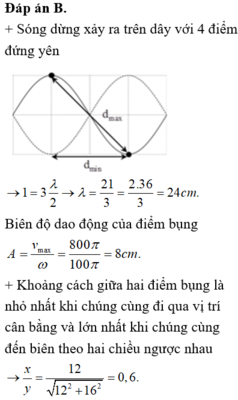
+ Sóng dừng xảy ra trên dây với 4 điểm đúng yên
→ l = 3 λ 2 → λ = 2 l 3 = 2 . 36 3 = 24 cm .
→ Biên độ dao động của điểm bụng
A = v max ω = 800 π 100 π = 8 cm .
+ Khoảng cách giữa hai điểm bụng là nhỏ nhất khi chúng cùng đi qua vị trí cân bằng và lớn nhất khi chúng cùng đến biên theo hai chiều ngược nhau.
→ x y = 12 12 2 + 16 2 = 0 , 6 .

Đáp án B
+ Sóng dừng xảy ra trên dây với 4 điểm đứng yên → l = 3 λ 2 → λ = 2 l 3 = 2.36 3 = 24 cm.
→ Biên độ dao động của điểm bụng A = v m a x ω = 800 π 100 π = 8 cm.
+ Khoảng cách giữa hai điểm bụng là nhỏ nhất khi chúng cùng đi qua vị trí cân bằng và lớn nhất khi chúng cùng đến biên theo hai chiều người nhau.
→ x y = 12 12 2 + 16 2 = 0 , 6

+ Trên dây có 2 bụng sóng nên: λ = 2 l k = 2.24 2 = 24 cm
+ Khi dây duỗi thẳng thì M, N chia dây làm 3 đoạn bằng nhau nên: AM = MN = NB = 8 cm.
+ MNmin = MN = 8 cm.
+ MNmax = MN’ = 8 2 + N N ' 2
® M N max M N min = 64 + N N ' 2 8 = 1 , 25 ® NN’ = 6 cm.
® A b ung = 2 3 cm
ü Đáp án C

Đáp án C.
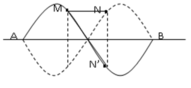
Trên dây có sóng dừng với hai bụng sóng nên
![]() .
.
M, N thuộc hai bó sóng liên tiếp nên ngược pha nhau.
Khoảng cách MN nhỏ nhất khi M, N ở vị trí cân bằng hay
![]() .
.
Gọi trung điểm MN là O (khi đó chính là một nút) thì OM = 4cm = λ/6.
Vậy biên độ dao động của M và N là:
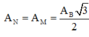 (vì M và N đối xứng nhau qua nút biên độ dao động bằng nhau).
(vì M và N đối xứng nhau qua nút biên độ dao động bằng nhau).
Khoảng cách M, B lớn nhất là
![]() khi M, N nằm ở biên.
khi M, N nằm ở biên.
Mặt khác
![]()
![]() .
.

Ta có $\lambda =24cm $
Bạn vẽ hình ra .
Đoạn AB =24cm sau đó vẽ 2 bụng sóng.
Lấy M N nằm giữa sao cho MN= AB/3 = 8 cm.
Khoảng cách MN lớn nhất khi chúng nằm trên bụng và nhỏ nhất khi duỗi thẳng.
Ta có $\dfrac{MN_{lớn}}{MN_{nhỏ}} =1.25 \rightarrow MN_{lớn}=10 \rightarrow $biên độ của M và N là 3cm.
Khoảng cách từ M đến nút bằng 4cm =$\dfrac{\lambda}{6} \rightarrow A_{bụng} =2\sqrt{3}$

Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.

Đây em nhé Câu hỏi của Nguyễn Thị Trúc Đào - Vật lý lớp 12 | Học trực tuyến