Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài sân trường hcn là x
chiều rộng sân trường hcn là y
ĐK: x,y > 0
Theo đề bài ta có hệ:
\(\hept{\begin{cases}x-y=16\\2x-5y=-28\end{cases}}\)(Nhân -5 cho pt đầu)
\(\Leftrightarrow\hept{\begin{cases}-5x+5y=-80\\2x-5y=-28\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-3x=-108\\x-y=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=36\\36-y=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=36\\y=20\end{cases}}\left(n\right)\)
Mình giải theo cách lập phương trình, bạn có thể tham khảo ạ!
Gọi chiều dài sân trường hcn là: x(x>16;m)
Vậy chiều rộng sân trường hcn là: x-16(m)
Vì hai lần chiều dài kém năm lần chiều rộng 28m, nên ta có phương trình
5(x-16)-2x=28
<=> 5x-80-2x=28
<=>3x=108
<=>x=36(TM)
Vậy chiều dài sân trường hcn là 36m
Chiều rộng sân trường hcn là 36-16=20m

Gọi x, y (m) lần lượt là chiều rộng và chiều dài của sân trường.
Điều kiện: 0 < x < 170; 0 < y < 170.
Vì chu vi của sân trường bằng 340 m nên ta có: 2(x + y) = 340
Vì ba lần chiều dài hơn bốn lần chiều rộng là 20m nên ta có: 3y – 4x = 20
Ta có hệ phương trình:
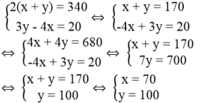
Giá trị của x và y thỏa điều kiện bài toán.
Vậy chiều rộng của sân trường là 70m,
chiều dài của sân trường là 100m.

Câu trả lời:
Gọi chiều dài và chiều rộng sân trường lần lượt là x và y ( 0<x,y<170 ; x>y)
Vì chu vi là 340 nên ta có PT: x+y=170 (1)
Vì 3 lần chiều dài lớn hơn 4 lầm chiều rộng 20 m nên ta có PT:
3x - 4y = 20 (2)
Từ (1) và (2) ta có HPT :
\(\left\{{}\begin{matrix}x+y=170\\3x-4y=20\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x=100\\y=70\end{matrix}\right.\)
Vậy chiều dài là chiều rộng sân trường lần lượt là 100m và 70m.
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của sân trường(Điều kiện: a>0; b>0)
Vì chu vi của sân trường là 340m nên ta có phương trình:
2(a+b)=340
\(\Leftrightarrow a+b=170\)(1)
Vì 3 lần chiều dài hơn 4 lần chiều rộng là 20m nên ta có phương trình:
3a-4b=20(2)
Từ (1) và (2) ta có được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=170\\3a-4b=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=510\\3a-4b=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7b=490\\a+b=170\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=70\\a=170-70=100\end{matrix}\right.\)(thỏa ĐK)
Vậy: Chiều dài của sân trường là 100m; Chiều rộng của sân trường là 70m

Lời giải:
Gọi chiều dài là $a$ và chiều rộng là $b$ (m)
Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=340:2=170\\ 3a-4b=20\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=100\\ b=70\end{matrix}\right.\) (m)

Nửa chu vi hình chữ nhật: 194 : 2 = 97 (m)
Gọi chiều dài là: x (m) (0 < x < 97)
Chiều rộng là: y (m) (0 < x < 97)
Nửa chu vi là 97 nên ta có phương trình:
x + y = 97 (1)
4 lần chiều dài hơn 5 lần chiều rộng là 10m, nên ta có phương trình:
4x - 5y = 10 (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=97\\4x-5y=10\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=55\left(TM\right)\\y=42\left(TM\right)\end{matrix}\right.\)
Vậy chiều dài và chiều rộng sân trường lần lượt là: 55m và 42m

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có hệ phương trình:
a+b=340/2=170 và 3a-4b=20
=>3a+3b=510 và 3a-4b=20
=>7b=490 và a+b=170
=>b=70 và a=100

Chiều dài là X chiều rộng là X-16.
có 5(X-16)-2X=28 <=>3X=28+80=108<=>X=36