Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi chiều rộng = a => chiều dài = a+10
Áp dụng định lý Pytago => a^2 + (a+10)^2 = độ dài đường chéo ^2 = 1300
=> 2a^2 +20a +100=1300
=> a^2 +10a-600 = 0
=> (a+30)(a-20) =0
=> a=20
=> chu vi sân bóng = 2(a+a+10) = 2.50 =100

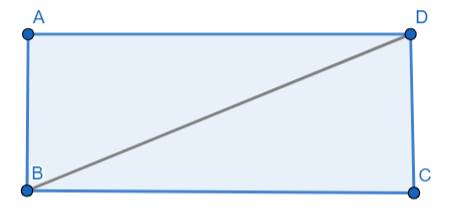
Ta có: \(AD=3AB\)
Xét tam giác vuông ABD ta có:
\(AD^2+AB^2=BD^2\)
\(\Rightarrow60^2=\left(3AB\right)^2+AB^2\)
\(\Rightarrow3600=9AB^2+AB^2\)
\(\Rightarrow3600=10AB^2\)
\(\Rightarrow AB^2=360\)
\(\Rightarrow AB=6\sqrt{10}\left(m\right)\)
\(\Rightarrow AD=3\cdot6\sqrt{10}=18\sqrt{10}\left(m\right)\)
Diện tích sân bóng là:
\(AB\cdot AD=6\sqrt{10}\cdot18\sqrt{10}=1080\left(m^2\right)\)

Gọi a là chiều rộng của sân bóng (m), chiều dài sân bóng là a+37 (m) (a>0)
Vì diện tích sân bóng là 7140m2, nên ta có:
a. (a+37)= 7140
<=> a2 + 37a - 7140= 0
<=> a= 68 (nhận) hoặc a= -105 (loại)
Vậy chiều rộng sân bóng là 68m, chiều dài sân bóng là 105m

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có hệ phương trình:
a-b=9 và (a+2)(b+1)=ab+50
=>a-b=9 và a+2b=48
=>a=22 và b=13

Lời giải:
Gọi chiều dài và chiều rộng sân bóng lần lượt là $a$ và $b$. Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=25\\ (a+5)(b+5)=ab+150\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a+b=25\\ 5(a+b)+25=150\end{matrix}\right.\Leftrightarrow a+b=25\)
Vậy từ dữ kiện đề ta chỉ thu được $a+b=25$ thôi nên không tính được $S$ lúc đầu bạn ạ.

Gọi chiều dài và chiều rộng của sân bóng lần lượt là \(x,y\left(m\right);x,y>0\).
Vì chu vi là \(140m\)nên \(2\left(x+y\right)=140\Leftrightarrow x+y=70\)
Vì giảm chiều rộng đi \(5m\)tăng chiều dài thêm \(8m\)thì diện tích sân bóng không đổi nên
\(\left(x+8\right)\left(y-5\right)=xy\Leftrightarrow-5x+8y=40\)
Ta có hệ phương trình:
\(\hept{\begin{cases}x+y=70\\-5x+8y=40\end{cases}}\Leftrightarrow\hept{\begin{cases}5x+5y=350\\-5x+8y=40\end{cases}}\Leftrightarrow\hept{\begin{cases}x=40\\y=30\end{cases}}\)(thỏa mãn)
Vậy chiều dài là \(40m\)chiều rộng là \(30m\).

Đây là sân bóng đá mini hình chữ nhật
gọi chiều dài là x m( x>0)
chiều rộng là x/2 m
theo đề ra ta có phương trình
2(x+x/2)=120
<=> x+x/2=60
<=> 3x=120
<=>x=40
vậy chiều dài sân bóng là 40
chiều rộng sânn bóng là 20
diện tích sân bóng là 40*20=800 m^2

Gọi chiều rộng là x
=>Chiều dài là x+10
Theo đề, ta có: x^2+(x+10)^2=50^2
=>2x^2+20x-2400=0
=>x^2+10x-1200=0
=>(x+40)(x-30)=0
=>x=30
Diện tích là 30*40=1200m2
Xét tg vuông ABH
\(BH=\sqrt{AB^2-AH^2}=\sqrt{18^2-14,4^2}=10,8m\)
Xét tg vuông ABD
\(AB^2=BH.BD\)(Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow BD=\frac{AB^2}{BH}=\frac{18^2}{10,8}=30m\)
Ta có
\(AD=\sqrt{BD^2-AB^2}=\sqrt{30^2-18^2}=24m\)