Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B.
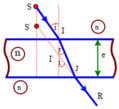
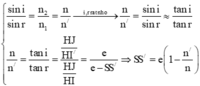
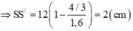
Kinh nghiệm: Dùng một bản mặt song song có chiết suất n có bề dày là e để nhìn vật thật S theo phương gần vuông góc với bản mặt thì bản mặt có tác dụng “dịch vật” theo chiều chiều của ánh sáng một đoạn:
1) 
nếu quan hệ đặt trong không khí.
2) 
nếu quang hệ đặt trong môi trưởng có chiết suất n.
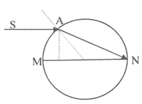
3/ \(n\sin i=\sin60^0;\) \(i=90-r\Rightarrow i=30^0\)
\(\Rightarrow n=\dfrac{\sin60^0}{\sin30^0}=\sqrt{3}\)
5/ \(D=\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow2=\dfrac{1}{0,25}+\dfrac{1}{d'}\Rightarrow d'=-50\left(cm\right)\)
\(k=-\dfrac{d'}{d}=\dfrac{50}{25}=2\)
=>D. Anh ao, cach thau kinh 50cm, k=2
7/ \(d=\dfrac{d'f}{d'-f}\Rightarrow d+d'=d'+\dfrac{d'f}{d'-f}=\dfrac{d'^2-d'f+d'f}{d'-f}=\dfrac{d'^2}{d'-f}\)
\(\left(d+d'\right)_{min}\Leftrightarrow(\dfrac{1}{d'}-\dfrac{f}{d'^2})_{max}\)
Dat \(\dfrac{1}{d'}=a\Rightarrow a-a^2f=-\left(a^2f+a+\dfrac{1}{4f}\right)+\dfrac{1}{4f}=-\left(a\sqrt{f}+\dfrac{1}{2\sqrt{f}}\right)^2\le\dfrac{1}{4f}\)
\("="\Leftrightarrow a\sqrt{f}=\dfrac{1}{2\sqrt{f}}\Leftrightarrow2af=1\Rightarrow a=\dfrac{1}{2f}\)
\(\Rightarrow\dfrac{1}{d'}=\dfrac{1}{2f}\Rightarrow d'=2f\Rightarrow d=\dfrac{d'f}{d'-f}=\dfrac{2f^2}{2f-f}=2f\)
\(\Rightarrow\left(d+d'\right)_{min}=2f+2f=4f\Rightarrow D.4f\)
8/ \(D=\dfrac{1}{f}=-\dfrac{1}{20}=-0,05\left(dp\right)\Rightarrow C.-0,05dp\)
15/ \(k_1=\dfrac{f}{f-d_1};k_2=\dfrac{f}{f-d_2};\dfrac{k_1}{k_2}=-1\)
\(d_2=d_1-12\Rightarrow\dfrac{k_1}{k_2}=-1=\dfrac{f-d_2}{f-d_1}=\dfrac{f-d_1-12}{f-d_1}\) (1)
\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};-\dfrac{d'_1}{d_1}=3\Rightarrow\dfrac{1}{f}=\dfrac{1}{d_1}-\dfrac{1}{3d_1}\)
\(\Rightarrow\dfrac{1}{f}=\dfrac{2}{3d_1}\Rightarrow d_1=\dfrac{2}{3}f\)
Thay vo (1)\(\Rightarrow\dfrac{f-\dfrac{2}{3}f-12}{f-\dfrac{2}{3}f}=-1\Leftrightarrow\dfrac{1}{3}f-12=-\dfrac{1}{3}f\Rightarrow f=18\left(cm\right)\)
19/ \(\sin i=n\sin r=n\cos i\Rightarrow\tan i=n\Rightarrow A.\tan i=n\)
22/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{20}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(-d'-d=45\Rightarrow d'=-d-45\Rightarrow\dfrac{1}{20}=\dfrac{1}{d}-\dfrac{1}{d+45}\)
\(\Leftrightarrow d^2+45d=45.20\Leftrightarrow\left[{}\begin{matrix}d=15\left(cm\right)\\d=-60\left(loai\right)\end{matrix}\right.\Rightarrow d'=-60\left(cm\right)\)
Vì khá lười vẽ hình nên mình sẽ lấy hình trên Internet nhé
Ta có: \(SS'=IM=e-MK\)
\(i=\widehat{IMS'}=\widehat{KMJ}\Rightarrow\tan i=\dfrac{KJ}{MK}\Rightarrow MK=\dfrac{KJ}{\tan i}\)
\(r=\widehat{I'JI}\Rightarrow\tan r=\dfrac{II'}{e}=\dfrac{KJ}{e}\)
\(\Rightarrow SS'=e-\dfrac{e\tan r}{\tan i}=e\left(1-\dfrac{\tan r}{\tan i}\right)\sim e\left(1-\dfrac{r}{i}\right)\)
\(i=n.r\Rightarrow SS'=6\left(1-\dfrac{1}{n}\right)=6\left(1-\dfrac{2}{3}\right)=2\left(cm\right)\)
\(\Rightarrow S'H=SH-SS'=20-2=18\left(cm\right)\)
