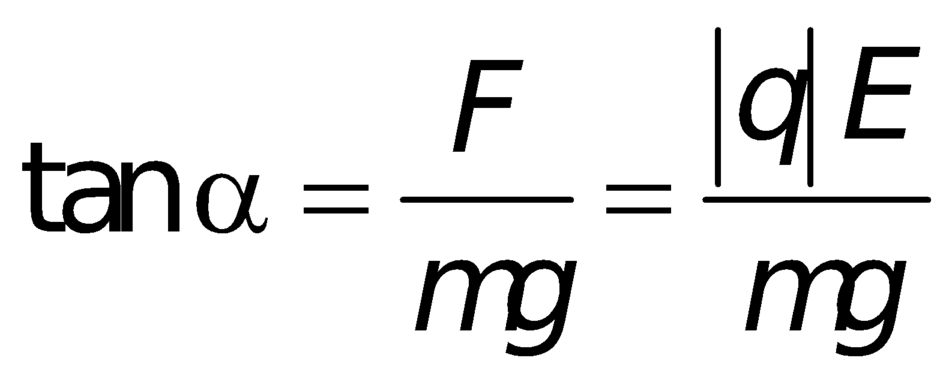Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án:
1154700V/m
Giải thích các bước giải:
Khi quả cầu cân bằng thì:
\(\tan a=\frac{F_d}{P}\Leftrightarrow\tan a=\frac{q^E}{mg}\\ E=\frac{\tan a.mg}{q}=1154700\left(V\text{/m}\right)\)

Điểm phải tìm nằm trong mặt phẳng chứa hai dòng điện, trong khoảng giữa hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm. Quỹ tích những điểm ấy là đường thẳng song song với hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm.

Điểm phải tìm nằm trong mặt phẳng chứa hai dòng điện, trong khoảng giữa hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm. Quỹ tích những điểm ấy là đường thẳng song song với hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm.

E P F
0,25g=2,5.10-4kg
\(\overrightarrow{T}=\overrightarrow{P}+\overrightarrow{F}\)
theo hình ta có
\(tan\alpha=\frac{F}{P}\Rightarrow F=m.g.tan\alpha\)
cường độ điện trường
\(E=\frac{F}{q}\approx839099N\)

Góc lệch \(\alpha\) của dây treo được xác định bằng hệ thức (suy từ điều kiện cân bằng của hai quả cầu :)
\(\tan\alpha=\frac{F_đ}{P}\)
Với \(F_đ=k\frac{q^2}{a^2}\) Như vậy \(\tan\alpha=\frac{kq^2}{mga^2}\)
Thay số ta được : \(\tan\alpha=1\) suy ra \(\alpha=45^o\)
mình chưa hiểu đoạn tan a = F/P lắm bạn giải thích lại hộ mình đc ko
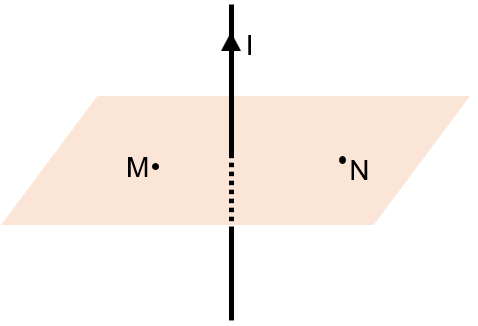
Khi hệ cân bằng: