Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có : 2BC - AB ≤ 2m.
- Mặt khác: BC.AB = 20m (1)
- Công suất lớn nhất khi:
BCmax ⇒ 2BC - AB = 2m (2)
- Từ (1) và (2) suy ra :
BC ≈ 3,7m; AB ≈ 5,4m.
- Dễ dàng tính được :
AM = 4,58m và A’M = 6,08m
- Tại người nghe được âm có mức cường độ âm lớn nhất là 13(B) = 130(dB):
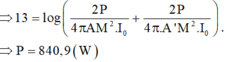

Đáp án C
Cường độ âm do các loa truyền đến điểm M :
I M = ( I N + I N ' ) ≡ P 2 π 1 a 2 + b 2 4 + 1 a 2 + b 2 4 + h 2
Để IM là lớn nhất thì biểu thức dưới mẫu phải nhỏ nhất. Ta có :
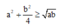 dấu bằng xảy ra khi
a
=
b
2
⇒
a
=
3
b
=
6
dấu bằng xảy ra khi
a
=
b
2
⇒
a
=
3
b
=
6
Giá trị cường độ âm khi đó
( I M ) m a x = 5 P m a x 108 π = 10
⇒ P m a x = 678 W

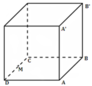
Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng

Đáp án A
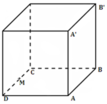
Để người ngối ở tâm nhà nghe rõ như 4 loa đặt ở góc tường thì cường độ âm do các loa nhỏ gây ra ở tâm bằng cường độ âm do loa ban đầu gây ra ở tâm nhà.
I = P 0 4 π R 2 = n P 4 π R 2 4
Với P 0 = 8 P , R là khoảng cách từ tâm nhà đến góc tường → 4n = 8 → n = 2.

Vì có điện trở thuần nên dao động trong mạch tắt dần do tỏa nhiệt ở điện trở. Để duy trì dao động điều hòa phải bổ sung cho mạch một năng lượng có công suất đủ bì vào phần năng lượng hao phí do tỏa nhiệt (hiệu ứng J un) trên điện trở, phần này có công suất là: \(\Delta P=I^2.R\)
Khi cùng cấp năng lượng đó, ta có: \(\frac{1}{2}CU^2_0=\frac{1}{2}LI^2_0\)
Mà: \(^{U=\frac{U_0}{\sqrt{2}}}_{I=I_{\frac{0}{\sqrt{2}}}}\)} \(\rightarrow I^2=\frac{C}{L}.U^2\)
\(P=I^2R=\frac{CR}{L}U^2=\frac{CRU^2_0}{2L}\)
\(\Rightarrow P=137\mu W\)
chọn B


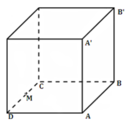

Đáp án A
Ta có : 2 B C - A B ≤ 2 m
Mặt khác : B C . A B = 20 m (1)
Công suất lớn nhất khi B C m a x ⇒ 2 B C - A B = 2 m (2)
Từ (1) và (2) suy ra : B C ≈ 3 , 7 m ; A B ≈ 5 , 4 m
Dễ dàng tính được : AM = 4,58m và A’M = 6,08m
Tại người nghe được âm có mức cường độ âm lớn nhất là 13(B) = 130(dB)
⇒ 13 = log ( 2 P 4 π A M 2 I 0 + 2 P 4 π A ' M 2 I 0 ) ⇒ P = 840 , 9 ( W ) .