Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định luật Cu lông ta có: \(F=k\frac{\left|q_1q_2\right|}{\varepsilon.r^2}\)
\(\Rightarrow r^2=9.10^9\frac{\left|10^{-7}.4.10^{-7}\right|}{\varepsilon.F}\)
a/ Trong không khí \(\varepsilon=1\)
\(\Rightarrow r^2=9.10^9\frac{\left|10^{-7}.4.10^{-7}\right|}{0,9}\)\(\Rightarrow r=0,02m=2cm\)
b/ Trong điện môi \(\varepsilon=4\)
\(\Rightarrow r^2=9.10^9\frac{\left|10^{-7}.4.10^{-7}\right|}{4.0,9}\)
\(\Rightarrow r=0,01m=1cm\)

Tính theo hai cách:
\(R=\frac{U}{I};R=\rho\frac{l}{S}\)
\(\rho\) là điện trở xuất của vật liệu
Suy ra: \(\rho=\frac{U}{I}\cdot\frac{S}{l}=\frac{ES}{I}\), trong đó có điện trường \(E=\frac{U}{l}\)
Cường độ dòng điện \(I\) đo bằng tổng điện lượng chạy qua diện tích \(S\) của đường dẫn trong 1 giây. Nếu \(v_{Na}\) và \(v_{CI}\) là tốc độ có hướng của các ion Na và CI, n là mật độ các ion này, thì ta có: \(I=eS\left(v_{Na}+v_{CI}\right)n=eS\left(\mu_{Na}+\mu_{CI}\right)nE\)
Suy ra: \(\rho=\frac{ES}{I}=\frac{1}{en\left(\mu_{Na}+\mu_{CI}\right)}\)
Với \(n=\frac{0,1mol}{l}=0,1\cdot6,023\cdot10^{23}\cdot10^3=6,023\cdot10^{25}\cdot m^{-3}\)
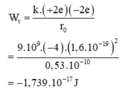
Khoảng cách của phân tử sau khi tích điện là: 0,459.10−6−0,459.10−6.1N
Độ cứng K cần tìm là:
\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = {9.10^9}\frac{{\left| { - 1,{{6.10}^{ - 19}}.1,{{6.10}^{ - 19}}} \right|}}{{81.{{(0,{{454.10}^{ - 6}})}^2}}} = 1380,{02.10^{ - 20}}N\)