Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đổi 54 km/h = 15 m/s
Chọn chiều dương là chiều chuyển động của xe. Như vậy, a = -1 m/s2
Thời gian hãm phanh cho tới lúc ô tô dừng lại là:
t = \(\dfrac{v-v_0}{a}=\dfrac{0-15}{-1}=15\left(s\right)\)
b) Quãng đường ô tô đi được trong thời gian hãm là:
s = \(\dfrac{\left(v_0\right)^2-v^2}{2a}=\dfrac{0^2-15^2}{2.-1}=112,5\left(m\right)\)

Ta có: \(v=v_0+at\)
Khi xe dừng hẳn thì: \(v_0+5a=0\left(1\right)\)
\(s=v_0.t+\dfrac{1}{2}at^2=5v_o+0,5.a.5^2=50\)
\(\Leftrightarrow5v_0+12,5a=50\left(2\right)\)
Từ (1) và (2) \(\Rightarrow v_0=20\)m/s
\(\Rightarrow a=-4\)m/s

Chọn gốc tọa độ, gốc thời gian lúc tàu bắt đầu hãm phanh, chiều dương là chiều chuyển động.
Ta có: v0 = 40 km/h = m/s; v = o
t = 2 phút = 120s
a) gia tốc: a = =
=
a = - 0,0925 m/s2.
b) Quãng đường tàu đi được: s = v0t +
=> s = x 120 -
≈ 667,3m
=> s ≈ 667,3m.
vo=40km/h=100/9 m/s; v=o; t=2'=120s
a=(v-v0)/t=-5/54(m/s2)
S=v0t+(at2)/2=2000/3=666,67(m)

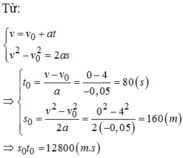
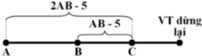
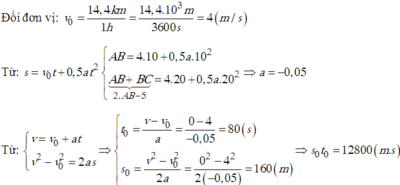
a, Chọn gốc tọa độ tai điểm xe bắt đầu hãm phanh, chiều dương cùng chiều chuyển động của xe, gốc thời gian là lúc xe bắt đầu hãm phanh.
\(v_0=54km/h=15m/s\)
\(\left\{{}\begin{matrix}s=v_0t+\frac{1}{2}at^2\\v^2-v_0^2=2as\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}s=600+800a\\as=-\frac{225}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}s=300\left(m\right)\\a=-0,375\left(m/s^2\right)\end{matrix}\right.\)
b, Phương trình chuyển động
\(x=x_0+v_0t+\frac{1}{2}at^2=600+800a\)