Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian t = s/v. Khi tăng vận tốc thành v’ = 1,5v thì thời gian là t' = s/1,5v
Tỉ số:
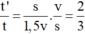
⇒ Đáp án A

thời gian tàu đi với vận tốc V1=\(\dfrac{27}{90}\)=0,3h
thời gian tàu đi với vận tốc v2=\(\dfrac{90-27}{72}\)=0,875h
sau thời gian 0,875+0,3=1,175 h thì tàu đến B
Vtb=\(\dfrac{S_1+S_2}{\dfrac{S_1}{90}+\dfrac{S_2}{72}}\)=\(\dfrac{90}{\dfrac{27}{90}+\dfrac{63}{72}}\)~76,6km/h
hihi mình cũng không biết đúng hay sai nữa bạn sửa giùm mình nha

Đổi:
8h30' = 8,5h
9h15' = 9,25h
30' = 0,5h
Thời gian ô tô đi hết quãng đường từ A đến B:
\(t_1=8,5-7=1,5h\)
Quãng đường AB dài:
s1 = v.t1 = 60.1,5 = 90km
Thời gian xe máy đã đi hết quãng đường từ A đến B:
t2 = 9,25 - 7 = 2,25h
Vận tốc xe máy:
v2 = \(\dfrac{s}{t_2}=\dfrac{90}{2,25}=40km/h\)
Khi ô tô nghỉ 30' thì thời gian xe máy đã đi:
t2' = 8,5 + 0,5 - 7= 2h
Quãng đường xe máy đã đi được khi ô tô nghỉ 30':
s2' = v2.t2' = 40.2 = 80km
Khoảng cách giữa xe máy với ô tô lúc này:
s3 = s - s2' = 90 - 80 = 10km
Quãng đường ô tô đi được đến lúc gặp nhau:
s4 = v1.t = 60t km
Quãng đường xe máy đi được đến lúc gặp nhau:
s5 = v2.t = 40t km
Ta có: s4 + s5 = s3
=> 60t + 40t = 10
=> 100t = 10
=> t = 0,1h = 6 phút
Vậy khi từ B trở về A ô tô gặp xe máy lúc 9h6'

a, Thời gian đi xe máy từ A là
\(t=t_1+t_2=\dfrac{s_1}{v_1}+\dfrac{s_2}{v_2}=\dfrac{AB}{2v_1}=\dfrac{AB}{2v_2}=\dfrac{AB}{30}\)
Thời gian xe ô tô đi từ B:
\(AB=v_1.\dfrac{t}{2}+v_2.\dfrac{t}{2}=t\left(\dfrac{v_1}{2}+\dfrac{v_2}{2}\right)=40t\\ \Rightarrow30t_{xe.máy}=49t_{xe.ô.tô}\\ \Rightarrow t_{xm}=\dfrac{4}{3}t_{xôt}\)
Mà
\(t_{xm}=t_{xôt}+0,5\left(30'=0,5h\right)\\ \Rightarrow\left\{{}\begin{matrix}t_{xôt}=1,5\left(h\right)\\t_{xm}=2\left(h\right)\end{matrix}\right.\\ \Rightarrow AB=60km\\ \Rightarrow\left\{{}\begin{matrix}v_{xm}=30\left(km/h\right)\\v_{xôt}=40\left(kmh/\right)\end{matrix}\right.\)
b, Xét thời gian 2 xe đổi \(v\)
\(t_{xôt}=\dfrac{t_{xm}}{2}=0,75\left(h\right)\\ t_{xm}=\dfrac{AB}{2v_1}=1,5\left(h\right)\)
Xe ô tô đổi vận tốc trước :
\(t=0,75\left(h\right)\)
2 xe còn cách nhau :
\(=69-2v_1.0,75=30\left(km\right)\)
Từ t = 0,75(h)
\(\rightarrow Xe.ô.tô.đi.với.v_2,xe.máy.vẫn.v_1\)
2 xe gặp nhau sau :
\(t=\dfrac{30}{\left(v_1+v_2\right)}=0,5\left(h\right)\)
Xe máy đi thêm được \(0,5.v_1=10\left(km\right)\)
Điểm gặp nhau cách A số km là
\(15+10=25\left(km\right)\)

10m/s=36km/h
ta có:
do cả hai lần cùng đi một quãng đường nên:
S=S1
\(\Leftrightarrow vt=v_1t_1\)
\(\Leftrightarrow36t=40t_1\)
mà t=t1+0,5
\(\Rightarrow36\left(t_1+0,5\right)=40t_1\)
\(\Rightarrow t_1=4,5h\)
\(\Rightarrow S=180km\)

\(=>S1=50t\left(km\right)\) (qđ xe từ A)
\(=>S2=40t\left(km\right)\)(qđ xe từ B)
\(=>30+40t=50t=>t=3h\)
=>kể từ khi 2 xe xuất phát sau 3h thì gặp nhau
vị trí gặp nhau cách A \(Sa=S1=50.3=150km\)
Hai xe xuất phát cùng một lúc nên gọi thời gian chuyển động của hai xe là t
Gọi v1 là vận tốc của ô tô 1; v2 là vận tốc của ô tô 2
Xe đi từ A có đường đi là s1 = v1t = 40t
Hai xe chuyển động cùng chiều từ A đến B nên lúc đầu xe B cách A một đoạn s0 = 20km
Xe đi từ B cách A một đoạn đường là: s2 = s0 + v2t = 20 + 30t (km)
Khoảng cách giữa hai xe: Δs = s2 - s1 = 20 + 30t - 40t = 20 - 10t (km)
\(\dfrac{t'}{t}=\dfrac{s}{2v}\cdot\dfrac{v}{s}=2\)
Thời gian giảm đi 2 lần.
2