Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số cách chia tổ thành 3 nhóm đi làm 3 công việc khác nhau là C 12 4 . C 8 4 . C 4 4 = 34650
Với công việc thứ nhất có C 9 3 C 3 1 cách chọn 3 nam, 1 nữ.
Với công việc thứ nhất có C 6 3 C 2 1 cách chọn 3 nam, 1 nữ.
Với công việc thứ nhất có C 3 3 C 1 1 cách chọn 3 nam, 1 nữ.
Vậy xác suất cần tính là P = C 9 3 C 3 1 . C 6 3 C 2 1 . C 3 3 C 1 1 C 12 4 C 8 4 C 4 4 = 16 55

Đáp án A
Không gian mẫu: C 12 4 . C 8 4 . 1 = 34650
Chỉ có 3 nữ và chia mỗi nhóm có đúng 1 nữ và 3 nam.
Nhóm 2 có C 3 1 . C 9 3 = 252 cách.
Lúc đó còn lại 2 nữ, 6 nam, nhóm thứ 2 có :
C 2 1 . C 9 3 = 40 cách chọn.
Cuối cùng còn 4 người là một nhóm: có 1 cách.
Theo quy tắc nhân thì có: 252.40.2=10080 cách.
Vậy xác suất cần tìm là: P = 10080 34650 = 16 55 .


Gọi A: “mỗi nhóm có đúng một học sinh nữ”.
+) Số cách xếp 3 học sinh nữ vào 3 nhóm là 3! cách.

+) Chọn 3 học sinh nam cho nhóm thứ ba có 1 cách.
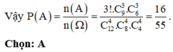

Đáp án D
Xác suất cần tìm là C 8 3 C 5 1 + C 8 4 C 5 + 8 4 = 70 143 .

Đáp án D
Số cách lập nhóm gồm 4 người là: C 13 4 = 715
Số cách lập nhóm gồm 4 người trong đó có 3 nữ là: C 8 3 . C 5 1 = 280
Số cách lập nhóm gồm 4 người trong đó có 4 nữ là: C 8 4 = 70
Vậy xác suất để lập nhóm 4 người trong đó có ít nhất 3 nữ là: p = 280 + 70 715 = 70 143





T a có \(\Omega\)" chọn 4 người"
\(\left|\Omega\right|=C^4_{12}\)
Gọi A" CHọn 4 người có đúng 1 người nữ'
suy ra có 3 người nam và 1 người nữ
\(\left|A\right|=C^1_3.C^3_9\)
XS để chọn đc 4 người nam và có 1 người nữ là:
\(P\left(A\right)=\frac{\left|A\right|}{\left|\Omega\right|}=\frac{C^1_3.C_9^3}{C^4_{12}}\)
Mình tính ra kq khác huhu. Sai chỗ nào v ạ