Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Gọi x; y lần lượt là số phẩm loại A; B.
Theo đề bài ta có: 2000x + 4000y = 40 000 hay x + 2y = 20
Suy ra: x = 20 - 2y.
Ta có 
Xét hàm 
Tập xác định D = (0; 10).
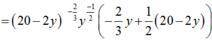
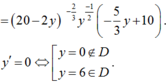
Nhận xét: 
nên dấu của y’ là dấu của biểu thức 
Do đó hàm số đạt giá trị lớn nhất khi y = 6 và x = 8
Vậy 
Giá của x sản phẩn là:
x ( 120 -x ) = - x2 +120x
Lợi nhuận còn lại:
\(-x^2+120x-C\left(x\right)=-x^2+120x-x^2-5x-300=-2x^2+115x-300\)
a)
Xác suất lấy được phế phẩm:
\(H=35\%.1\%+40\%.1,5\%+0,8\%.25\%=1,15\%\)
b) Sp máy I: 35%.1%= 0,35%
Sp máy 2: 40%.1,5%= 0,6%
Sp máy 3: 0,8%.25%=0,2%
=> Kết luận...(Em tự so sánh nè)
Lời giải:
Theo bài ra ta có \(m^{\frac{2}{3}}n^{\frac{1}{3}}\geq 40\Rightarrow m^2n\geq 40^3\)
Số chi phí phải trả mỗi ngày là:
\(P=6m+24n\). Ta cần tìm min \(P\)
Áp dụng BĐT Cauchy ta có:
\(P=3m+3m+24n\geq 3\sqrt[3]{3m.3m.24n}=3\sqrt[3]{216m^2n}\geq 3\sqrt[3]{216.40^3}=720\)
Vậy \(P_{\min}=720(\text{USD})\) tức là chi phí ít nhất mỗi ngày phải trả là \(720 (\text{USD})\)
đồng
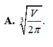
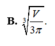
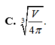
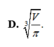
Ta có x ∈ (0; 60000)
Do đó, hàm số đạt cực tiểu tại x = 50000.
Nên x=50000 là số sản phẩm cần sản xuất mỗi ngày để tối thiểu chi phí.
Chọn C