Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
Vì truyền tải điện năng cần $2$ dây dẫn nên: \(R=\rho\frac{2l}{S}=3\left(\Omega\right)\)
Công suất hao phí: \(\Delta P=I^2R=\left(\frac{P}{U.\cos\varphi}\right)^2R=\frac{250000}{27}W\)
Suy ra hiệu suất truyền tải là \(H=\frac{P-\Delta P}{P}=98,15\%\)
Xin lỗi mình tính nhầm, vẫn công thức như bài giải dưới, kết quả là $94%$
Chọn đáp án B
h 1 = 1 - H 1 = P 1 R U 2 cos 2 φ h 2 = 1 - H 2 = P 2 R U 2 cos 2 φ ⇒ 1 - H 2 1 - H 1 = P 2 P 1 ⇒ 1 - H 2 1 - 0 , 8 = 3 4 ⇒ H 2 = 0 , 85
Hao phí truyền tải điện: \(P_{hp}=10\%.P= 0,1.P=20kW=20000W\)
Ta có: \(P_{hp}=I^2.R=I^2.200=20000\Rightarrow I = 10A\)
Chọn A.
GIẢI THÍCH:
| P |
U |
ΔP |
P’ |
| 8 |
U |
8 – 6 = 2 |
75%.8 = 6 |
| x |
U |
|
81,25%.6 = 4,875 |
Chọn A.
GIẢI THÍCH:
Gọi công suất mỗi tổ máy là P0.
Ban đầu công suất phát: P1 = 8P0; công suất tiêu thụ là: P 1 ' = 0 , 7 P 1 ;
Hao phí: 
.
Công suất tiêu thụ giảm:
Công suất phát lúc này:
Giải phương trình Ta được: P2/P1 = 2,71 hoặc P2/P1 = 0,63.
Để giảm hao phí thì P2/P1 = 0,63 Þ P2 » 5P0.
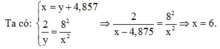
Chọn A.
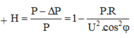
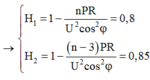
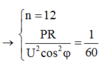
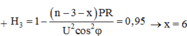
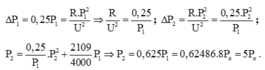
Đáp án B
Gọi số tổ máy ban đầu là n (tổ). Công suất mỗi máy là a (W). Ta có :
- Ban đầu :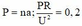
- Sau khi rút 3 tổ máy
- Sau khi rút x tổ máy để đạt hiệu suất 95% :
Từ (1) và (2) ta có
Từ (1) và (3) ta có
Suy ra phải rút tổng cộng 9 tổ máy mới đạt hiệu suất 95% => phải rút thêm 6 tổ máy nữa