Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

E A B E M C xe thứ nhất xe thứ 2
Theo đề ta có:
Đoạn FE là
FE= 200. 2= 400 (km)
Vận tốc xe thứ 3 là:
50. 2= 100 ( km)
Quang đường xe thứ 3 nhiều hơn xe thứ 2 là;
200 + 10= 210 ( km)
Hiệu của hai vận tốc là:
100- 4= 60 ( km)
Thời gian 2 xe gặp nhau và gấp đôi xe thứ hất là:
210 : 60=3,5 ( giờ)
Khoảng cách đến C của xe thứ nhất gấp đôi xe thứ 2 cần số giờ là:
7 + 3,5= 10,5 ( giờ)
Đổi 10,5 giờ= 10 giờ 30 phút
Vậy: Khoảng cách đến C của xe thứ nhất gấp đôi xe thứ 2 cần 10 giờ 30 phút

Gọi x là quãng đường AB
x-0,5 là quãng đường BC
2h30'=2,5h
Vận tốc đi trên quãng đường AB là: \(\frac{x}{2,5}\)
Vận tốc đi trên quãng đường BC là: \(\frac{x}{2,5}+1=\frac{2,5+x}{2,5}\)
mặt khác vận tốc đi trên đoạn BC còn =\(\frac{x-0,5}{2}\)
=> \(\frac{2,5+x}{2,5}=\frac{x-0,5}{2}\)
<=> 50 + 20x = 25x - 12,5
<=> 5x= 62,5
<=> x= 12,5(km)
=> đoạn AB dài 12,5(km)
=> đoạn BC dài 12(km)
=> đoạn AC dài 24,5(km)

Đáp án C
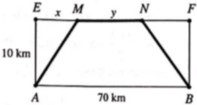
B M = x k m , 0 < x < 25 ta có
A M = A B 2 + B M 2 = x 2 + 100 = x 2 + 100 k m , M C = B C − B M = 25 − x k m
Thời gian bạn A đi xe buýt từ nhà đến điểm hẹnM là t A = x 2 + 100 30 h
Thời gian bạn A, B đi xe máy từ điểm hẹn M đến nhà bạn C là t A B = 25 − x 50 h
Suy ra thời gian bạn A đi từ nhà đến nhà bạn C là t x = t A + t A B = x 2 + 100 30 + 25 − x 50 h
Để bạn A đến nhà bạn C nhanh nhất thì hàm số t(x) đạt giá trị nhỏ nhất, với 0 < x < 25
Ta có t ' x = x 30 x 2 + 100 + 1 50 ; t ' x = 0 ⇔ x = 15 2
Lập bảng biến thiên, ta thấy hàm số t(x) đạt giá trị nhỏ nhất bằng t 15 2 = 23 30 h khi x = 15 2 k m = B M ⇒ M C = 25 − x = 35 2 k m .
Khi đó 5 B M + 3 M C = 5. 15 2 + 3. 35 2 = 90

Đáp án C
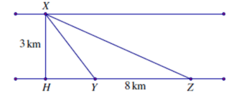
Đặt H Y = x 0 ≤ x ≤ 8 khi đó thời gian người đó đến Z là: f x = 1 6 9 + x 2 + 1 8 8 − x
f ' = x 6 9 + x 2 − 1 8 = 4 x − 3 9 + x 2 24 9 + x 2 ⇒ f ' = 0 ⇔ x = 9 7
⇒ M i n f = M i n f 0 ; f 8 ; f 9 7 = M i n 3 2 ; 73 6 ; 7 8 + 1 = 1 + 7 8

Em giải đúng chưa thầy giáo hoc24 ?
giải :
Thời gian Nam đi đến trường là:
14 : 5 = 2,8 ( giờ ) = 2 giờ 48 phút
Lúc Nam đến trường là lúc:
7 giờ 30 phút + 2 giờ 48 phút = 10 giờ 18 phút
Thời gian anh Nam đến trường là:
14 : 12 = 7/6 giờ = 70 phút
Anh Nam phải xuất phát lúc:
10 giờ 18 phút - 70 phút = 9 giờ 8 phút
Đ/s: 9 giờ 8 phút


Đáp án B
Phân tích:
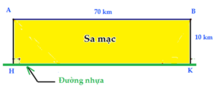
● Ta có thể mô tả bài toán trên bằng hình vẽ sau:
● Như đã phân tích ở trên, nếu đi trực tiếp từ A đến B trên sa mạc với vận tốc và khoảng cách hiện có thì nhà địa chất học không thể đến đúng thời gian quy định
● Vì vậy cần thiết phải chia quãng đường đi được thành 3 giai đoạn:
Giai đoạn 1: đi từ A đến C (từ sa mạc đến đường nhựa song song)
Giai đoạn 2: đi từ C đến D (một quãng đường nào đó trên đường nhựa)
Giai đoạn 3: đi từ D đến B (từ điểm kết thúc D trên đường nhựa đi tiếp đến B băng qua sa mạc).
Goi H, K, C, D là các điểm như hình vẽ.