Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Tổng số vân sáng trong khoảng rộng L là: N = 17 + 3 = 20 (vân sáng).
Số vân sáng của bức xạ λ 1 trong khoảng rộng L là:
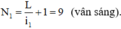
Số vân sáng của bức xạ λ 2 là:
N 2 = N - N 1 = 20 - 9 = 11 (vân sáng).
Bạn tham khảo ở đây nhé: Câu hỏi của Thu Hà - Vật lý lớp 12 | Học trực tuyến
Cách giải: Đáp án B
Do khoảng cách giữa hai vân sáng kề nhau bằng khoảng vân i, nên nếu trên trường giao thoa rộng L mà có hai vân sáng nằm ở hai đầu thì trường đó sẽ được phủ kín bởi các khoảng vân i, số khoảng vân được cho bởi N = L/2 và số vân sáng quan sát được trên trường là N’ = N + 1.
Số vân sáng đếm được trên trường (các vân trùng nhau chỉ tính một vân) là 25 vân, trong 25 vân này có 5 vạch trùng nhau nên số vân thực tế là kết quả giao thoa của hai bức xạ là 30 vân sáng.
Số khoảng vân ứng với bước sóng λ1 là N 1 = L i 1 = 32 / 2 = 16
→ số vân sáng ứng với λ1 là N1’ = 17 vân.
Khi đó, số vân sáng ứng với bước sóng λ2 là N2’ = 30 – 17 = 13 vân,
Số vân sáng của ánh sáng λ2 quan sát được trên màn là 13 – 5 = 8 vân
Đáp án B
Do khoảng cách giữa hai vân sáng kề nhau bằng khoảng vân i, nên nếu trên trường giao thoa rộng L mà có hai vân sáng nằm ở hai đầu thì trường đó sẽ được phủ kín bởi các khoảng vân i, số khoảng vân được cho bởi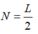 
và số vân sáng quan sát được trên trường là N’ = N + 1.
Số vân sáng đếm được trên trường (các vân trùng nhau chỉ tính một vân) là 25 vân, trong 25 vân này có 5 vạch trùng nhau nên số vân thực tế là kết quả giao thoa của hai bức xạ là 30 vân sáng.
Số khoảng vân ứng với bước sóng λ1 là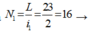 
số vân sáng ứng với λ1 là N1’ = 17 vân
Khi đó, số vân sáng ứng với bước sóng λ2 là N2’ = 30 – 17 = 13 vân,
Số vân sáng của ánh sáng λ2 quan sát được trên màn là 13 – 5 = 8 vân
\(i_1=\dfrac{\lambda_1.D}{a}=1,2mm\)
Số vân sáng của i1 là: \(|\dfrac{24}{2.1,2}|.2+1=21\)
Số vân sáng của i2 là: \(33+5-21=17\)
\(\Rightarrow i_1=1,5mm\)
\(\Rightarrow \lambda_2=0,75\mu m\)
Theo đề bài: Với bức xạ λ1 thì 10i1 = MN = 20mm → i1 = 2mm.
\(\frac{\iota_1}{\iota_2}=\frac{\text{λ}_1}{\text{λ}_2}=\frac{3}{5}\)\(\rightarrow\iota_2=\frac{10}{3}mm\rightarrow N_2=2.\left[\frac{MN}{2\iota_2}\right]+1=7\)
Khoảng vân ứng với bước sóng \(\lambda\) là:
\(i=\lambda\frac{D}{d}=k\lambda\) (với \(k=\frac{D}{d}\))
Vân sáng trung tâm là cực đại chung của cả 3 bước sóng.
Cực đại chung gần nhất ứng với khoảng cách là bội chung nhỏ nhất của 3 khoảng vân.
Để đơn giản, ta tìm bội chung nhỏ nhất của 42, 56, 63. Mình sẽ hướng dẫn luôn.
Trước hết phân tích thành tích các số nguyên tố:
\(\text{42=7×2×3 }\)
\(56=7\text{×}2^3\)
\(63=7\text{×}3^2\)
Bội chung nhỏ nhất là: \(7\text{×}2^3\text{×}3^2=504\)
Vậy khoảng giữa 2 vân sáng liên tiếp có màu giống màu vân trung tâm là:\(d=5,04k\left(m\right)\)
Bội chung nhỏ nhất giữa 42 và 56 là: \(\text{7×}2^3\text{×}3=168\)
Suy ra trong khoảng \(d\) có 2 vân sáng là : \(\lambda_1\) và \(\lambda_2\) trùng nhau
Bội chung nhỏ nhất giữa 42 và 63 là: \(7\text{×}2\text{×}3^2=126\)
Suy ra trong khoảng \(d\)có 3 vân sáng là \(\lambda_1\) và \(\lambda_3\) trùng nhau.
Bội chung nhỏ nhất giữa 56 và 63 là: \(7\text{×}2^3\text{×}3^2=504\)
Suy ra trong khoảng \(d\) có 0 vân sáng là \(\lambda_2\) và \(\lambda_3\) trùng nhau.
Vậy tổng số vân sáng bên trong khoảng d là:
\(\frac{d}{i_1}-1+\frac{d}{i_2}-1+\frac{d}{i_3}-1-2-3-0\)
\(=\frac{504}{42}-1+\frac{504}{56}-1+\frac{504}{63}-1-2-3-0\)
\(=21\) (vân sáng )
----> chọn A
ta có:
\(i_1:i_2:i_3=\lambda_1:\lambda_2:\lambda_3=6:8:9\)
Bội chung nhỏ nhất là 72
Như vậy vân 12 của bức xạ 1 trùng với 9 của bx2 và 8 của bx3
trong khoảng này thì bx2 và và bx3 không trùng cực đại vì 8 và 9 nguyên tố cùng nhau
cực đại số 4 và số 8 của bx1 trùng với cực đại số 3 và 6 của bx2
cực đại số 3 ,6 và số 9 của bx1 trùng với cực đại số 2; 4và 6 của bx2
Số cực đại nhìn thấy là
11+8+7-2-3=21
\(\rightarrow chọn.A\)
Bạn theo hướng bài này nhé Câu hỏi của Thu Hà - Vật lý lớp 12 | Học trực tuyến
Số vân sáng quan sát được là
\(N_s = N_{s1}+ N_{s2}-N_{trung nhau} =17.\)
Số vân sáng của \(\lambda_1\) trên trường giao thoa L là
\(N_{s1}= 2.[\frac{L}{2i_1}]+1 = 9.\)
=> \(N_{s2}= N_s-N_{s1}-N_{trung nhau} = 17-9+3=11.\)
B .11