Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Phương pháp: Viết phương trình dao động của phần tử môi trường tại M và xét đặc điểm của nó
Cách giải:
Phương trình dao động của nguồn O là: u 0 = 2 cos ( 20 π t + π 3 ) m m
Phương trình dao động của phần tử bất kì là:
u m = 2 cos ( 20 π ( t - d m v ) + π 3 ) = 2 cos ( 20 π t - 20 π d m v + π 3 ) mm
Biết dm < 42,5 cm. và vận tốc v = 1m/s = 100cm/s.
Phần tử m dao động lệch pha π/6 so với nguồn tức là:
20 π d m v = π 6 + k 2 π ⇔ 20 π . d m 100 = π 6 + k 2 π ⇔ d m 5 = 1 6 + 2 k ⇔ d m = 5 6 + ' 10 k
Áp dụng điều kiện 0 < dm < 42,5 cm ta có : 0 < 10 k + 5 6 < 42 , 5 ⇔ - 0 , 08 < k < 4 , 1 ⇒ k = 0 , 1 , 2 , 3 , 4
Vậy có 5 giá trị k thỏa mãn.
Làm theo cách cơ bản ta có độ lệch pha:
\(\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{\pi}{6}+k2\pi\) với \(\lambda=6cm\)
Ta có : .
Vậy có 5 điểm
C đúng
Đáp án B
+ Ta có : Bước sóng λ = v t = 1 20 π 2 π = 0 , 1 m = 10 c m
+ Độ lệch pha giữa một điểm nằm trên phương truyền sóng và phần tử ở nguồn O là :
△ φ = 2 π d λ
+ Theo bài : △ φ = π 6 ⇒ 2 π △ d λ = π 6 ⇒ △ d = λ 12
+ Lại có : 42,5=4 λ + λ 4
+ Trên phương truyền sóng hai điểm cách nhau λ thì cùng pha => từ O đến M có 4 điểm dao động cùng pha với O
+ Vì ở đây cho điểm H dao động cùng pha với O và chậm pha hơn O1 góc π 6 nên ta có hai bó cùng pha sẽ là hai bó chẵn hoặc là hai bó lẻ . Vậy những điểm cùng pha với O chậm hơn nằm trên bó 1,3,5 , trong 1 bó sẽ có 2 điểm dao động chậm pha hơn hai bó nguyên ( có 4 điểm ) và một phần λ 4 của bó 5 ( có 1 điểm nửa)
=> có tất cả là 5 điểm
Hướng dẫn: Chọn đáp án B
Kinh nghiệm: Bài toán cho x1 và xu hướng đang tăng (v1 > 0) hoặc đang giảm (v1 <0) thì nên làm theo cách 2.
Cách 1: Viết lại phương trình li độ vận tốc:
Cách 2: Chọn trạng thái tại thời điểm t1 là trạng thái ban đầu Þj= p/6 Pha dao động ở thời điểm tiếp theo:
Hướng dẫn: Chọn đáp án C
Độ lệch pha của một điểm trên MN cách O một khoảng d là:
Đổi: \(v=1\)m/s\(=100\)cm/s
\(\omega=20\pi\Rightarrow f=10Hz\Rightarrow\lambda=\dfrac{v}{f}=\dfrac{100}{10}=10cm\)
Chọn điểm N bất kì trên OM lệch pha \(\dfrac{\pi}{3}\) với nguồn.
\(\Rightarrow\Delta\varphi_{ON}=\dfrac{2\pi x}{\lambda}=\dfrac{\pi x}{5}=\pm\dfrac{\pi}{3}+k2\pi\Rightarrow k=\dfrac{x}{10}\mp\dfrac{1}{6}\left(k\in Z\right)\)
Giờ thì ta giải từng cái một thooi^.^
Nếu \(k=\dfrac{x}{10}+\dfrac{1}{6}\Rightarrow0\le x\le42,5\)
\(\Rightarrow0\le10k\le\dfrac{10}{6}< 42,5\Rightarrow0,17\le k\le4,42\)
\(\Rightarrow k\) nhận 4 giá trị
Nếu \(k=\dfrac{x}{10}-\dfrac{1}{6}\Rightarrow0\le x\le42,5\)
\(\Rightarrow0\le10k+\dfrac{10}{6}\le42,5\Rightarrow-0,17\le k\le4,083\)
\(\Rightarrow k\) nhận 5 giá trị.
Vạy khoảng từ O đến M có \(4+5=9\) điểm dao động lệch pha \(\dfrac{\pi}{3}\) với nguồn.
Đổi: v=1v=1m/s=100=100cm/s
ω=20π⇒f=10Hz⇒λ=vf=10010=10cmω=20π⇒f=10Hz⇒λ=vf=10010=10cm
Chọn điểm N bất kì trên OM lệch pha π3π3 với nguồn.
⇒ΔφON=2πxλ=πx5=±π3+k2π⇒k=x10∓16(k∈Z)⇒ΔφON=2πxλ=πx5=±π3+k2π⇒k=x10∓16(k∈Z)
Giờ thì ta giải từng cái một thooi^.^
Nếu k=x10+16⇒0≤x≤42,5k=x10+16⇒0≤x≤42,5
⇒0≤10k≤106<42,5⇒0,17≤k≤4,42⇒0≤10k≤106<42,5⇒0,17≤k≤4,42
⇒k⇒k nhận 4 giá trị
Nếu k=x10−16⇒0≤x≤42,5k=x10−16⇒0≤x≤42,5
⇒0≤10k+106≤42,5⇒−0,17≤k≤4,083⇒0≤10k+106≤42,5⇒−0,17≤k≤4,083
⇒k⇒k nhận 5 giá trị.
Vạy khoảng từ O đến M có 4+5=94+5=9 điểm dao động lệch pha π3π3 với nguồn.
Đáp án D
Tần số sóng: 
Bước sóng 
Những điểm vuông pha với nguồn có độ lệch pha:
=> khoảng cách đến nguồn là
và d>0.
ÞSố điểm = số giá trị của k nguyên:
có 13 điểm vuông pha với nguồn
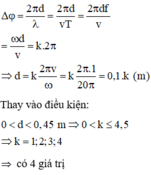
Đáp án A