

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án A
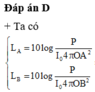
+ Ta có
![]()
→ O A = O B . 10 ∆ L 20 = 200 m
→ Thời gian chuyển động của người t = O A - O B v = 90 s

Câu hỏi này bạn cần biết phân tích chuyển động biến đổi đều của xe, quãng đường xe chuyển động và âm chuyển động để giải bài toán.
+ Biết mức cường độ âm tại N lớn hơn mức cường độ âm tại M là 20 dB, ta có:
\({{L}_{N}}-{{L}_{M}}=10.\lg{{\left( \dfrac{{{R}_{M}}}{{{R}_{N}}} \right)}^{2}}=20\Rightarrow {{R}_{M}}=OM=10{{R}_{N}}=100m\)
\(\Rightarrow MN = OM – ON = 90 m\)
Vật (thiết bị) đi từ M nhanh dần đều đến trung điểm của MN, sau đó chuyển động chậm dần và dừng lại tại N, nên ta có: \({{t}_{MN}}=2.{{t}_{MC}}\)(C là trung điểm của MN)
\(MC=\dfrac{MN}{2}=\dfrac{1}{2}at_{MC}^{2}\Rightarrow {{t}_{MC}}=\sqrt{\dfrac{MN}{a}}\)
\(\Rightarrow t={{t}_{MN}}=2\sqrt{\dfrac{MN}{a}}=2\sqrt{\dfrac{90}{04}}=30s\)
Vậy giá trị gần nhất là 32s

Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng

+ Ta có: LN - LM = 20 dB → 10 log P 4 π O N 2 . I 0 - 10 log P 4 π O M 2 . I 0 = 20
→ O M O N = 10 → OM = 100 m → MN = 90 m.
+ Vì thiết bị chuyển động với 2 giai đoạn nên ta có thể coi một giai đoạn chuyển động nhanh dần đều với a = 0,4 m/s2 và một giai đoạn chuyển động chậm dần đều với gia tốc 0,4 m/s2 đến khi dừng lại tại N.
* Giai đoạn 1 ta có: v2 - 0 = 2as1 → s 1 = v 2 2 a
* Giai đoạn 2 ta có: 0 - v2 = -2as2 → s 2 = v 2 2 a
Mà s1 + s2 = MN = 90 m → v = 6 m/s.
+ v = 0 + at1 → t1 = 15 s
+ 0 = v - at2 → t2 = 15 s
→ t = 30 s gần với giá trị của đáp án B nhất.
Đáp án B