Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Xét phép thử: “Chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có bốn chữ số”
Ta có 
Biến cố A: “Số được chọn có ít nhất hai chữ số 8 đứng liền nhau”.
Gọi số có 4 chữ số a b c d ¯ là trong đó có ít nhất hai chữ số 8 đứng liền nhau, a ≠ 0
TH1: Có đúng hai chữ số 8 đứng liền nhau.
+) Số có dạng 88 c d ¯ : có 9.9 = 81 số.
+) Số có dạng a 88 d ¯ hoặc a b 88 ¯ : mỗi dạng có 8.9 = 72 số.
TH2: Có đúng ba chữ số 8 trong đó có ít nhất hai chữ số 8 đứng liền nhau.
+) Số có dạng a 888 ¯ : có 8 số.
+) Số có dạng 8 b 88 ¯ hoặc 88 c 8 ¯ hoặc 888 d ¯ : Mỗi dạng có 9 số.
TH3: Cả 4 chữ số đều là chữ số 8: Có 1 số là số 8888
Do đó n(A) = 81 + 2.72 + 8 + 3.9 + 1 = 261
Xác suất cần tìm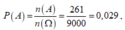 
Chọn C
Cách 1: Số các số tự nhiên có hai chữ số phân biệt là 9.9 = 81 số.
Số phần tử của không gian mẫu là 
Gọi A là biến cố thỏa mãn bài toán.
+ Khả năng 1: Hai bạn chọn số giống nhau nên có 81 cách.
+ Khả năng 2: Hai bạn chọn số đảo ngược của nhau nên có 9.8 = 72 cách.
+ Khả năng 3: Hai bạn chọn số chỉ có một chữ số trùng nhau
- TH1: Trùng chữ số 0: Công có 9 cách chọn số và Thành đều có 8 cách chọn số nên có 9.8 = 72 cách.
- TH 2: Trùng chữ số 1: Nếu Công chọn số 10 thì Thành có 16 cách chọn số có cùng chữ số 1. Nếu Công chọn số khác 10, khi đó Công có 16 cách chọn số và Thành có 15 cách chọn số có cùng chữ số 1 với Công nên có 16 + 16.15 = 16.16 256 cách.
- Các trường hợp chọn trùng chữ số 2,3,4,....,9 tương tự.
Vậy 
Xác suất cần tính là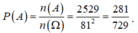 
Cách 2: Số các số tự nhiên có hai chữ số phân biệt là 9.9= 81 số.
Số phần tử của không gian mẫu là 
Gọi là biến cố thỏa mãn bài toán. Xét biến cố A ¯
- TH 1: Công chọn số có dạng a 0 ¯ nên có 9 cách. Khi đó có 25 số có ít nhất một chữ số trùng với số a 0 ¯ nên Thành có 81 - 25 = 56 cách chọn số không có chữ số trùng với Công. Vậy có 9.56 = 504 cách.
- TH 2: Công chọn số không có dạng a 0 ¯ : Có 72 cách, khi đó 32 số có ít nhất một chữ số trùng với số của Công chọn nên Thành có 81 - 32 = 49 cách chọn số không có chữ số nào trùng với Thành. Vậy có 72.49 = 3528 cách.
Chọn C
Số các số tự nhiên có hai chữ số phân biệt là 9.9 = 81 số.
Số phần tử của không gian mẫu là 
Gọi A là biến cố “Hai chữ số được viết ra có ít nhất một chữ số chung”
Khi đó ta có biến cố A ¯ là “Hai chữ số được viết ra không có chữ số chung”
Gọi hai chữ số mà Công và Thành viết ra lần lượt là a b ¯ v à c d ¯
- TH1: b = 0, khi đó a có 9 cách, c có 8 cách và d có 7 cách. Vậy có 9.8.7 = 504 cách viết.
- TH2: b ≠ 0, khi đó a có 9 cách, b có 8 cách, c có 7 cách và d có 7 cách. Vậy có 9.8.7.7 = 3528 cách viết.
cách viết.
Vậy xác suất của biến cố A là:
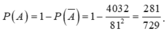
Nhận xét: Đây là một bài toán xác suất chọn số. Đối với bài toán này, ta sẽ đi theo hướng tính gián tiếp thông qua phần bù. Khi đó cách làm sẽ ngắn hơn và tránh nhầm lẫn không đáng có.
Đáp án B
Phương pháp: Xét các trường hợp:
TH1: a1 + a2 = a3 + a4 = a5 + a6 = 5
TH2: a1 + a2 = a3 + a4 = a5 + a6 = 6
TH3: a1 + a2 = a3 + a4 = a5 + a6 = 7
Cách giải:
TH1: a1 + a2 = a3 + a4 = a5 + a6 = 5, ta có 0 + 5 = 1 + 4 = 2 + 3
- Nếu (a1;a2) = (0;5) => có 1 cách chọn (a1a2)
Có 2 cách chọn (a3a4), 2 số này có thể đổi vị trí cho nhau nên có 4 cách chọn.
Tương tự (a5a6) có 2 cách chọn.
=> Có 8 số thỏa mãn.
- Nếu (a1;a2) ↓ (0;5) => có 2 cách chọn (a1a2), 2 số này có thể đổi vị trí cho nhau nên có 4 cách chọn.
Có 2 cách chọn (a3a4), 2 số này có thể đổi vị trí cho nhau nên có 4 cách chọn.
Tương tự (a5a6) có 2 cách chọn.
=> Có 32 số thỏa mãn.
Vậy TH1 có: 8 + 32 = 40 số thỏa mãn.
TH2: a1 + a2 = a3 + a4 = a5 + a6 = 6, ta có 0 + 6 = 1 + 5 = 2 + 4 = 6.
Tương tự như TH1 có 40 số thỏa mãn.
TH3: a1 + a2 = a3 + a4 = a5 + a6 = 7, ta có 1 + 6 = 2 + 5 = 3 + 4 = 7
Có 3 cách chọn (a1a2), hai số này có thể đổi chỗ cho nhau nên có 6 cách chọn.
Tương tự có 4 cách chọn (a3a4) và 2 cách chọn (a5a6).
Vậy TH3 có 6.4.2 = 48 số thỏa mãn.
Vậy có tất cả 40 + 40 + 48 = 128 số có 6 chữ số khác nhau thỏa mãn a1 + a2 = a3 + a4 = a5 + a6
Để viết một số có 6 chữ số khác nhau bất kì có 6.6.5.4.3.2 = 4320 số.
Vậy P = 128 4320 = 4 135 .
Đáp án B
Gọi 
là số cần tìm, để số này chia hết cho 4 thì ta phải có 
chia hết cho 4.
Có 
số tự nhiên có 4 chữ số tạo từ 
.
Ta thấy chỉ có các số 
là chia hết cho 4.
Do đó chọn 
có 7 cách, chọn a có 6 cách, chọn b có 7 cách nên có 
Vậy xác suất cần tính là 
Chọn A
Gọi số tự nhiên có bốn chữ số thỏa mãn yêu cầu bài toán là 
Số phần tử của không gian mẫu là 
Gọi biến cố A ‘‘Số được chọn lớn hơn số 6700’’.
Ta các TH sau:
TH1: có 1 cách chọn.
có 3 cách chọn.
+ Các chữ số c,d được chọn từ 8 chữ số còn lại có sắp thứ tự và số cách chọn là A 8 2
Số cách để chọn ở trường hợp 1 là: 3. A 8 2
TH2 : 
có 3 cách chọn. Khi đó: b,c,d có
A
9
3
cách chọn.
Số cách để chọn ở trường hợp 1 là: 3. A 9 3
Như vậy, ta được n(A) = 3. A 8 2 + 3. A 9 3 = 1680
Suy ra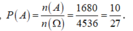 
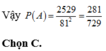
Không gian mẫu: \(9.10.10.10=9000\)
Số cách viết thỏa mãn: \(C_{10}^4=210\)
Xác suất: \(P=\dfrac{210}{9000}=...\)