Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Vận tốc viên gạch bằng 0 tại độ cao cực đại.
Áp dụng công thức
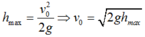
![]()

Tóm tắt: \(h=4\left(m\right);\\ g=10\left(\dfrac{m}{s^2}\right);\\ v=?\)
Giải: Vận tốc ném viên gạch là
ADCT: \(v^2=2.g.h=2.10.4=80\)
\(\Rightarrow v=\sqrt{80}=4\sqrt{5}\approx8,94\left(\dfrac{m}{s}\right)\)
Một người thợ xây ném một viên gạch theo phương thẳng đứng cho một người khác ở trên tầng cao 4m.Người này chỉ việc giơ tay ngang ra là bặt được viên gạch. Lấy g=10m/s2 . Để cho viên gạch lúc người kia bắt được bằng không thì vận tốc ném là bao nhiêu
Giải :
Vận tốc ném viên đá là :
v2 = 2.g.h
=> v2 = 80m/s
=> v = \(\sqrt{80=8,944...191\approx8,94}\)m/s

\(v^2-v_o^2=2gh\)
\(\Leftrightarrow0-10^2=2\cdot\left(-10\right)h\)
\(\Leftrightarrow h=5\left(m\right)\)

Áp dụng định luật bảo toàn cơ năng ta có Wmặt đất=Wvị trí cực đại
<=>m*v^2/2=m*g*z<=>100=20*z<=>z=5
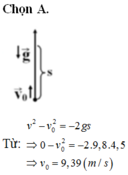
Chọn đáp án D
Chọn gốc tọa độ tại vị trí ném, chiều dương hướng lên.
Áp dụng công thức độc lập thời gian và kết hợp điều kiện tại h = 4m thì v = 0 ta có: