Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
Chọn chiều dương là chiều chuyển động của hai vật
Người và xe va chạm mềm. Gọi v 1 , v 2 , V lần lượt là vận tốc của người, xe lúc trước và của xe lúc sau va chạm. Ta có:
m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 = 50.3 + 150.2 50 + 150 = 2 , 25 m / s
Đáp án: B

Áp dụng định luật bảo toàn động lượng :
→pt=→ps��→=��→ <=> m1→v1=m2→v2�1�1→=�2�2→
=> m1→v1+m2→v2=→v(m1+m2)�1�1→+�2�2→=�→(�1+�2)
<=> →v=m1→v1+m2→v2m1+m2�→=�1�1→+�2�2→�1+�2
chọn chiều dương là chiều chuyển động ban đầu của xe
a)Cùng...

Ta xét toa xe + người. Khi người nhảy lên toa goòng ( theo phương ngang) với vận tốc \(\overrightarrow{V1}\), ngoại lực tác dụng lên hệ là trọng lực \(\overrightarrow{P}\) và phản lực đàn hồi \(\overrightarrow{N}\) của mặt đường
Vì các vật trong hệ chuyển động theo phương ngang nên các ngoại lực ( đều có phương thẳng đứng ) sẽ cân bằng nhau. Như vậy hệ ta khảo sát có thể coi là hệ kín. Áp dụng định luật bảo toàn động lượng ta có:
\(m1.\overrightarrow{V1}+m2.\overrightarrow{V2}=\left(m1+m2\right).\overrightarrow{V''}\) (1)
trong đó \(\overrightarrow{V''}\) là vận tốc của toa goòng sau khi người nhảy lên toa.
a)a) Trường hợp 1: ban đầu người và toa chuyển động cùng chiều. Chiếu (1) trên trục OxOx nằm ngang có chiều dương là chiều \(\overrightarrow{V2}\) và \(\overrightarrow{V1}\) ta có
\(m1.V1+m2.V2=\left(m1+m2\right).\overrightarrow{V''}\)
\(\Rightarrow V''\frac{m1.v1+m2.v2}{m1+m2}=2,25m/s>0\)
Toa goòng tiếp tục chuyển động theo chiều cũ với vận tốc 2,25m/s
b) Trường hợp 2: ban đầu người và toa goòng chuyển động ngược chiều.
chiếu (1) lên trục Ox như trên ta có
\(-m1.v1+m2.v2=\left(m1+m2\right)V''\)
suy ra \(V''=\frac{-m1.v1+m2.v2}{m1+m2}=0,75m/s>0\)
Toa goòng tiếp tục chuyển động theo chiều cũ với vận tốc 0,750,75m/s

chọn chiều dương cùng chiều chuyển động của xe
\(\overrightarrow{v_1}.m_1+\overrightarrow{v_2}.m_2=\overrightarrow{V}.\left(m_1+m_2\right)\)
b) xe, người chuyển động cùng chiều
\(\Rightarrow v_1.m_1+v_2.m_2=V.\left(m_1+m_2\right)\)
\(\Rightarrow V=\)\(\dfrac{44}{13}\)m/s
b)xe, người chuyển động ngược chiều
\(\Rightarrow-v_1.m_1+v_2.m_2=V.\left(m_1+m_2\right)\)
\(\Rightarrow V=\)\(\dfrac{4}{13}\)m/s

Chọn chiều (+) là chiều chuyển động của xe.
a. Theo định luật bảo toàn động lượng ta có:
( m 1 + m 2 ) v = m 1 ( v 0 + v ) + m 2 v 2 ⇒ v 2 = ( m 1 + m 2 ) v − m 1 . ( v 0 + v ) m 2 = ( 60 + 100 ) .3 − 60 ( 4 + 3 ) 100 = 0 , 6 ( m / s )
b. Theo định luật bảo toàn động lượng ta có:
( m 1 + m 2 ) v = m 1 ( v − v 0 ) + m 2 v 2 ⇒ v 2 = ( m 1 + m 2 ) v − m 1 . ( v − v 0 ) m 2 = ( 60 + 100 ) .3 − 60 ( 3 − 4 ) 100 = 5 , 4 ( m / s )

Lời giải
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của hai vật
Gọi v 1 , v 2 , V lần lượt là vận tốc của người, xe trước và xe sau va chạm. Ta có:
m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 ⇔ 1 , 625 = 50.5 + 150. v 2 50 + 150 ⇔ v 2 = 0 , 5 m / s
Đáp án: A


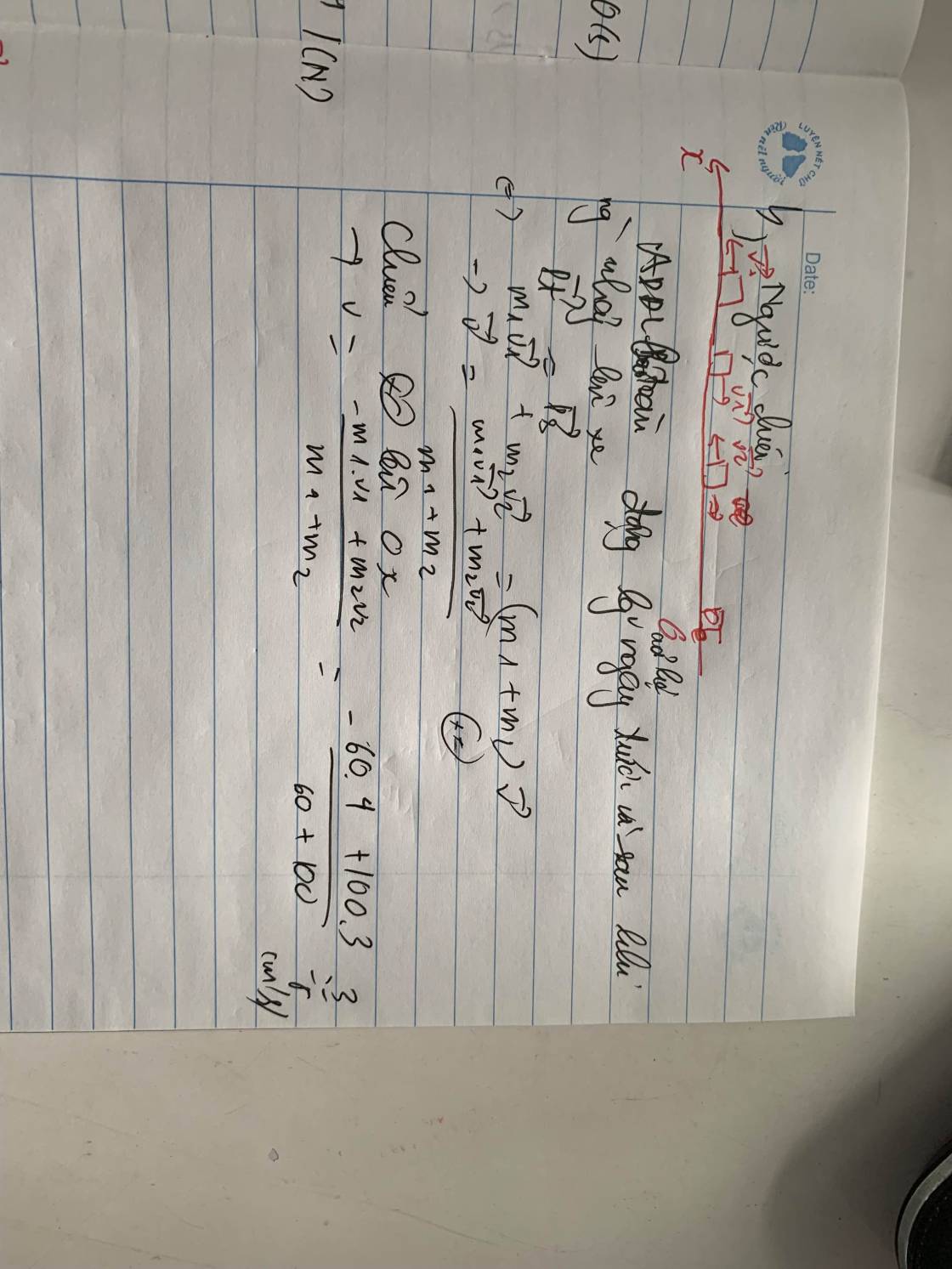

Lời giải
Chọn chiều dương là chiều chuyển động của người
Người và xe va chạm mềm. Gọi v 1 , v 2 , V lần lượt là vận tốc của người, xe lúc trước và của xe lúc sau va chạm. Ta có:
m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇔ V = m 1 v 1 + m 2 v 2 m 1 + m 2 = 50.3 − 150.2 50 + 150 = − 0 , 75 m / s
Với v 2 = - 150 m / s vì xe chuyển động ngược chiều so với người
Vậy độ lớn của xe sau va chạm là 0,75 m/s
Đáp án: D