Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có ![]()
Suy ra sau 19 năm thì số tiền sẽ lớn hơn 300 triệu

HD: Số tiền cả gốc lẫn lãi của người đó sau n năm là: T = 100(1 + 6%)n
Để số tiền nhiều hơn 300 triệu thì:
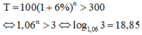
Vậy sau ít nhất 19 năm người đó nhận được số tiền nhiều hơn 300 triệu. Chọn A.

Đáp án C
Áp dụng công thức lãi kép: A n = A 1 + r n
Với A n , y M ' = là số tiền nhận được sau n năm (cả gốc và lãi).
A là tiền gốc.
n là số năm gửi.
r là lãi suất hằng năm.
Cách giải:
Sau n năm người đó nhận được A n = 75 1 + 5,4 100 n > 100 ⇔ n > 5,47
Vậy sau ít nhất 6 năm người đó nhận được số tiền nhiều hơn 100 triệu đồng.

Đáp án C
Để số tiền người đó nhận được nhiều hơn 130 triệu đồng bao gồm gốc và lãi thì
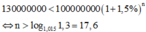
Vậy sau ít nhất 18 quý người đó nhận được số tiền nhiều hơn 130 triệu đồng bao gồm gốc và lãi.

Đáp án A
Cuối tháng thứ n, người đó có số tiền cả gốc lẫn lãi là T n = a m 1 + m n − 1 1 + m
Với a là số tiền gửi vào hàng tháng, m là lãi suất mỗi tháng và n là số tháng gửi
Theo bài ra, ta có 3 0 , 06 % . 1 + 0 , 06 % n − 1 1 + 0 , 06 % > 100 ⇔ 1 , 006 n > 603 503 ⇔ n > 30 , 3 tháng
Vậy sau ít nhất 31 tháng thì anh A có được số tiền lớn hơn 100 triệu đồng.

Đáp án C
Gọi n là số năm cần gửi, suy ra 100 1 + 7 % n ≥ 250 ⇔ n ≥ 13,54 ⇒ n = 14

Đáp án A.
Phương pháp: Sử dụng công thức lãi kép.
Cách giải: Số tiền anh A nhận được sau n tháng là:
![]()
![]()
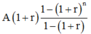

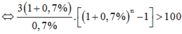
![]()
Vậy phải cần ít nhất 30 tháng để anh A có được nhiều hơn 100 triệu

Đáp án đúng : A