Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 30 phút = 30 60 = 1 2 (h).
Với quãng đường AB là x (km), thời gian người đó đi hết quãng đường lúc đi là: x 30 (h); thời gian người đó đi quãng đường AB lúc về là: x 24 (h).
Theo đề bài ta có phương trình x 24 - x 30 = 1 2
Đáp án cần chọn là: C

30 phút = (1/2) giờ
Gọi quãng đường AB là x (km). Điều kiện x > 0.
Thời gian xe máy đi từ A đến B là x/30 (giờ).
Thời gian xe máy đi từ B về A là x/24 (giờ).
Ta có phương trình:
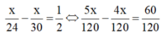
⇔ 5x - 4x = 60 ⇔ x = 60 (thỏa mãn điều kiện)
Vậy quãng đường AB là 60 km.

30 phút=\(\dfrac{1}{2}\)giờ
Gọi thời gian lúc đi là x(giờ; x>0)
Vì thời gian lúc đi ít hơn thời gian lúc về là 30 phút(\(\dfrac{1}{2}\)giờ)
=>Thời gian lúc về là:x+\(\dfrac{1}{2}\)(giờ)
Vận tốc của người đó lúc về nhỏ hơn vận tốc lúc đi là 6km/h
=>Vận tốc của người đó lúc về là:30-6=24(km/h)
Quãng đường lúc đi: 30x(km)
Quãng đường lúc về là: 24(x+\(\dfrac{1}{2}\))
Quãng đường đi được là không đổi nên ta có phương trình:
30x=24(x+\(\dfrac{1}{2}\))
\(\Leftrightarrow\)30x=24x+12
\(\Leftrightarrow\)30x-24x=12
\(\Leftrightarrow\)6x=12
\(\Leftrightarrow\)x=2(TMĐK)
Vậy quãng đường AB dài: 30.2=60km

Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Theo đề, ta có phương trình:
\(\dfrac{x}{24}-\dfrac{x}{30}=\dfrac{1}{2}\)
\(\Leftrightarrow x\cdot\dfrac{1}{120}=\dfrac{1}{2}\)
hay \(x=\dfrac{1}{2}:\dfrac{1}{120}=\dfrac{1}{2}\cdot120=60\left(thỏa\right)\)
Vậy: Độ dài quãng đường AB là 60km




