Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đổi 15 phút = 0,25 giờ
2 giờ 30 phút = 2,5 giờ
Gọi quãng đường đi từ A đến B là x ( km; x>0 )
Do người đó đi từ A đến B với vận tốc 50 km/h
=> t1 = \(\frac{x}{50}\)( h )
Do người đó đi từ B về A với vận tốc 40 km/h
=> t2 =\(\frac{x}{40}\)( h )
Lại có người đó nghỉ 15 phút nên ta có phương trình:
\(\frac{x}{50}+\frac{x}{40}+0,25=2,5\)
\(\Leftrightarrow\frac{4x}{200}+\frac{5x}{200}+\frac{50}{200}-\frac{500}{200}=0\)
\(\Leftrightarrow9x-450=0\)
\(\Leftrightarrow x=50\)( thỏa mãn điều kiện xác định )
Vậy chiều dài quãng đường AB là 50 km
Đổi \(15phút=\dfrac{1}{4}\left(h\right);2giờ30phút=\dfrac{5}{2}\left(h\right)\)
Gọi quãng đường AB là \(x\left(km;x>0\right)\)
Thì Thời gian người đó đi từ đến B là \(\dfrac{x}{50}\left(h\right)\)
Thời gian người đó quay về A là : \(\dfrac{x}{40}\left(h\right)\)
Vì đến B người đó nghỉ lại \(\dfrac{1}{4}h\) và thời gian tổng cộng là \(\dfrac{5}{2}h\) nên ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{50}+\dfrac{1}{4}=\dfrac{5}{2}\)
\(\Leftrightarrow5x+4x+50=500\)
\(\Leftrightarrow9x=450\)
\(\Leftrightarrow x=50\left(nhận\right)\)
Vậy độ dài quãng đường AB là \(50km\)
Gọi độ dài của quãng đường AB là \(x\left(km\right)\)
ĐK: \(x>0\)
Thời gian người đó đi từ A đến B là: \(\dfrac{x}{50}\left(h\right)\)
Thời gian người đó đi từ B về A là: \(\dfrac{x}{40}\left(h\right)\)
Đổi \(15p=\dfrac{1}{4}h;2h30p=\dfrac{5}{2}h\)
Theo đề ta có phương trình:
\(\dfrac{x}{50}+\dfrac{x}{40}=\dfrac{5}{2}-\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{x.4}{50.4}+\dfrac{x.5}{40.5}=\dfrac{5.100}{2.100}-\dfrac{1.50}{4.50}\)
\(\Leftrightarrow4x+5x=500-50\)
\(\Leftrightarrow9x=450\)
\(\Leftrightarrow x=50\left(tmđk\right)\)
Vậy quãng đường AB dài 50 km
Gọi độ dài AB là x
Thời gian đi là x/50
Thời gian về là x/40
=>x/50+x/40=2,25
=>x=50
Gọi quãng đường AB là x(km) (x>0)
Thời gian đi là:\(\dfrac{x}{30}\left(h\right)\)
Thời gian về là:\(\dfrac{x}{24}\left(h\right)\)
5h30p= 11/2 h
Theo đề bài ta có pt:
\(\dfrac{x}{30}+1+\dfrac{x}{24}=\dfrac{11}{2}\)
\(\Leftrightarrow x\left(\dfrac{1}{30}+\dfrac{1}{24}\right)=\dfrac{9}{2}\)
\(\Leftrightarrow x=60\left(tm\right)\)
Vậy quãng đường AB dài 60km
Gọi quãng đường `AB` là: `x` `(km)` `ĐK: x > 0`
`@` Thời gian lúc đi là: `x/30 (h)`
`@` Thời gian lúc về là: `x/24 (h)`
Đổi `5 h 30 ' = 11/2 h`
Vì thời gian tổng cộng hết `5 h 30'` nên ta có ptr:
`x/30+x/24+1=11/2`
`<=>[4x]/120+[5x]/120+120/120=660/120`
`<=>4x+5x+120=660`
`<=>9x=540`
`<=>x=60` (t/m)
Vậy quãng đường `AB` dài `60 km`
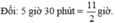
Tổng thời gian xe đi từ A đến B và đi từ B về A (không tính thời gian làm việc tại B) là: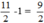 
(giờ)
Gọi độ dài quãng đường AB là x km (x >0)
Gọi quãng đường AB là x(km) (x>0)
Thời gian đi là:\(\dfrac{x}{30}\left(h\right)\)
Thời gian về là:\(\dfrac{x}{24}\left(h\right)\)
5 giờ 30 phút = 11/2 giờ
Theo đề bài ta có pt:
\(\dfrac{x}{30}+1+\dfrac{x}{24}=\dfrac{11}{2}\)
\(\Leftrightarrow\dfrac{x}{30}+\dfrac{x}{24}=\dfrac{9}{2}\)
\(\Leftrightarrow\dfrac{4x+5x}{120}=\dfrac{540}{120}\)
\(\Leftrightarrow9x=540\)
\(\Leftrightarrow x=60\left(tm\right)\)
Vậy quãng đường AB dài 60km
Gọi q/d `AB` là: `x(km)` `ĐK: x > 0`
`@` T/g lúc đi là: `x / 30` `(h)`
`@` T/g lúc về là: `x / 24` `(h)`
Đổi `5` giờ `30` phút `= 11 / 2 h`
Vì t/g tổng cộng hết `5` giờ `30` phút và đến `B` còn làm việc trong `1` giờ nên ta có ptr:
`x / 30 + x / 24 + 1 = 11 / 2`
`<=> [ 4x ] / 120 + [ 5x ] / 120 + 120 / 120 = 660 / 120`
`<=> 4x + 5x + 120 = 660`
`<=> 9x = 540`
`<=> x = 60` (t/m)
Vậy q/đ `AB` dài `60 km`
Gọi độ dài quãng đường AB là x
Thời gian đi là x/30
Thời gian về là x/24
Theo đề, ta có: x/30+x/24=5,5
=>x=220/3
Gọi độ dài quãng đường AB là x
Thời gian đi là x/30(h)
Thời gian về là x/25(h)
Theo đề, ta có:
\(\dfrac{x}{30}+\dfrac{x}{25}+\dfrac{1}{3}=5+\dfrac{5}{6}\)
=>x=75
Câu trả lời phải đợi duyệt vì có thể chứa từ ngữ không phù hợp lá sao nhỉ?
Thời gian đi: 2.5 - 0.25 = 2.25 h = 9/4 h
=> S/50 + S/40 = 9/4
=> 9S/200 = 9/4
=> S = 50km
Câu trả lời sao lại bị có từ ngữ không phù hợp và bị xóa nhỉ? Xóa thì nói rõ cho mình biết với.