Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

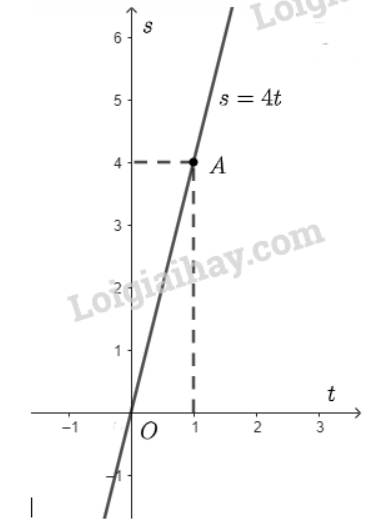
Với \(v = 4 \Rightarrow s = 4t\). Khi đó \(s\) là hàm số bậc nhất theo biến \(t\).
Với \(t = 1 \Rightarrow s = 4.1 = 4 \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;4} \right)\).
Đồ thị hàm số \(s = 4t\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;4} \right)\).

Cứ 1 giờ người đó lại đi được \(v\) km.
Cứ 2 giờ người đó lại đi được \(2v\)km.
Vậy sau \(t\left( h \right)\) người đó sẽ đi được quãng đường \(v.t\) km.
Vậy ta có công thức tính \(s\)theo \(t\) như sau: \(s = v.t\) trong đó \(v\) là vận tốc, \(t\) là thời gian và \(s\) là quãng đường đi được.

Ta có các biểu thức:
\(s=vt;v=\dfrac{s}{t};t=\dfrac{s}{v}\)
Tất cả đều là đơn thức không phải đa thức
`S = v.t; v = S/t; t = S/v`.
Không phải là đa thức.

a) Hàm số biểu thị quãng đường S(t) (km) mà ô tô đi được trong thời gian t (h) là: S = 60t (km)
b) Quãng đường S(t) (km) mà ô tô đi được trong thời gian t = 2 (h) là: S = 60. 2= 120 (km)
quãng đường S(t) (km) mà ô tô đi được trong thời gian t = 3 (h) là: S = 60. 3 = 180 (km)

a:
15p=1/4h
Độ dài quãng đường mà xe máy điện đi trước là:
\(40\cdot\dfrac{1}{4}=10\left(km\right)\)
Sau h giờ, xe máy đi được: 50h(km)
Sau h giờ, xe máy điện đã ở cách A: 10+40h(km)
Khoảng cách giữa xe máy và xe máy điện sau mỗi h giờ là:
40h+10-50h=-10h+10(km)
b: Hai người gặp nhau khi -10h+10=0
=>-10h=-10
=>h=1
Khi đó, vị trí hai người gặp nhau cáchA:
1*50=50(km)
vậy: Hai người gặp nhau sau 1 giờ và gặp tại vị trí cách A 50km
a:
15p=1/4h
Độ dài quãng đường mà xe máy điện đi trước là:
40⋅14=10(km)40⋅14=10(��)
Sau h giờ, xe máy đi được: 50h(km)
Sau h giờ, xe máy điện đã ở cách A: 10+40h(km)
Khoảng cách giữa xe máy và xe máy điện sau mỗi h giờ là:
40h+10-50h=-10h+10(km)
b: Hai người gặp nhau khi -10h+10=0
=>-10h=-10
=>h=1
Khi đó, vị trí hai người gặp nhau cáchA:
1*50=50(km)
vậy: Hai người gặp nhau sau 1 giờ và gặp tại vị trí cách A 50km

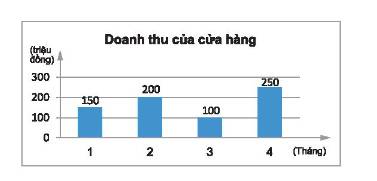
a) Đại lượng là hàm số là doanh thu (triệu đồng) của một cửa hàng và biến số là tháng x.
b) Đại lượng là hàm số là quãng đường đi được và biến số là thời gian .
c) Đại lượng là hàm số là số tiền người mua phải trả và biến số là số quyển vở.

| Vận tốc (km/h) | Quãng đường đi (km) | Thời gian đi (h) | |
| Xe máy | 35 | s | 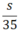 |
| Ô tô | 45 | 90 – s | 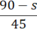 |
Ô tô xuất phát sau xe máy 2/5 giờ nên
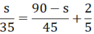

2 giờ 05 phút = \(\frac{25}{12}\)giờ
Gọi x ( km ) là đoạn đường đi bộ. x > 2,5
Đoạn đường đi xe là: x - 2,5 ( km )
Thời gian đi bộ là: \(\frac{6}{x}\)( h )
Thời gian đi xe là: \(\frac{25}{x-2,5}\)( h )
Theo đề ra ta có pt: \(\frac{6}{x}+\frac{25}{x-2,5}=\frac{25}{12}\)
Giải tiếp là ra
Hk tốt

Bài 1 :
a, Thời gian em học sinh đi từ nhà đến trường là :
\(t=\frac{S}{v}=\frac{4}{16}=0,25\left(h\right)\)
b, Đổi 0,25 h = 15 phút
Em học sinh đến trường lúc :
6h30phút + 15 phút = 6h45phút

a) Quãng được vật đi được với vận tốc 3 \(km/h\)trong khoảng thời gian \(t\) (giờ) là:
\(s = v.t = 3.t\).
b) Vẽ đồ thị hàm số \(s = 3.t\)
Cho \(t = 1 \Rightarrow s = 3.1 = 3\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(M\left( {1;3} \right)\).
Đồ thị hàm số \(s = 3.t\) là đường thẳng đi qua hai điểm \(O\) và \(M\).