Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc dự định đi là x (km/h) và thời gian dự định đi là b (h)
ĐK: x,b > 0
Theo đề bài, ta có:
\(\dfrac{60}{x}-\dfrac{60}{x+5}=1\)
\(\Leftrightarrow\) \(60\left(x+5\right)-60x=x\left(x+5\right)\)
\(\Leftrightarrow x^2+5x-300=0\)
\(\Leftrightarrow\left(x-15\right)\left(x+20\right)=0\)
\(\Leftrightarrow x=15\)
=> vận tốc dự định là 15 km/h
Thời gian dự định đi là: \(\dfrac{60}{15}=4\left(h\right)\)

vận tốc ban đầu người đó là x (km/h) (x>0)
khi về vận tốc người đó là x+5 (km/h)
Thời gian khi đi, khi về lần lượt là: \(\dfrac{60}{x}\left(h\right);\dfrac{60}{x+5}\left(h\right)\)
Vì thời gian về ít hơn thời gian đi 1h, nên ta có:
\(\dfrac{60}{x}=\dfrac{60}{x+5}+1\\ \Leftrightarrow\dfrac{60\left(x+5\right)}{x\left(x+5\right)}=\dfrac{60x+x\left(x+5\right)}{x\left(x+5\right)}\\ \Leftrightarrow60x+300=60x+x^2+5x\\ \Leftrightarrow x^2+60x-60x+5x-300=0\\ \Leftrightarrow x^2+5x-300=0\\ \Leftrightarrow x^2-15x+20x-300=0\\ \Leftrightarrow x\left(x-15\right)+20\left(x-15\right)=0\\ \Leftrightarrow\left(x-15\right)\left(x+20\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-15=0\\x+20=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=15\left(nhận\right)\\x=-20\left(loại\right)\end{matrix}\right.\)
Vậy: Vận tốc lúc đi của người ấy là 15(km/h)

gọi x là thời gian đi thì thời gian về là x+18[phút]
gọi y là quãng đường ab[km]
theo bài ra ta có hệ phương trình
\(25\cdot x=y\)
\(\left(25-5\right)\cdot\left(x+18\right)=y\)
từ hệ trên ta có \(25\cdot x=\left(x+18\right)\cdot20\)
suy ra x=72
đổi 72 phút = 1.2 giờ
suy ra quãng đường ab dài: \(25\cdot1,2=30km\)

Gọi vận tốc của người đi xe máy trên 3/4 quãng đường AB đầu (90 km) là x (km/h) (x > 0)
Vận tốc của người đi xe máy trên 1/4 quãng đường AB sau là 0,5x (km/h)
Vận tốc của người đi xe máy khi quay trở lại A là x + 10 (km/h)
Tổng thời gian của chuyến đi là 90 x + 30 0 , 5 x + 120 x + 10 + 1 2 = 8 , 5
⇔ 90 x + 60 x + 120 x + 10 = 8 ⇔ 150 x + 120 x + 10 = 8 ⇔ 75 ( x + 10 ) + 60 x = 4 x ( x + 10 ) ⇔ 4 x 2 − 95 x − 750 = 0 ⇔ x = 30 ( d o x > 0 )
Vậy vận tốc của xe máy trên quãng đường người đó đi từ B về A là 30 + 10 = 40 (km/h)

Gọi x (km/h) là vận tốc của người đi xe đạp từ A đến B (x >0)
x + 5 là vận tốc là vận tốc lúc đi từ B về A
Thời gian mà người đó đi từ A đến B: \(\frac{60}{x}\) (h)
Thời gian mà người đó đi từ B về A: \(\frac{60}{x+5}\) (h)
Vì thời gian lúc về ít hơn thời gian đi là 1 giờ nên ta có phương trình:
\(\frac{60}{x}-\frac{60}{x+5}=1\) (ĐKXĐ: \(x\ne0\); \(x\ne-5\))
\(\Leftrightarrow\frac{60x+300-60x}{x\left(x+5\right)}=\frac{x^2+5x}{x\left(x+5\right)}\)
\(\Leftrightarrow x^2+5x-300=0\)
\(\Leftrightarrow x^2-15x+20x-300=0\)
\(\Leftrightarrow\left(x-15\right)\left(x+20\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=15\left(nhan\right)\\x=-20\left(loai\right)\end{cases}}\)
Vậy vận tốc của người đó đi từ A đến B là 15km/h
Gọi x (km/h) là vận tốc của người đi xe đạp từ A đến B (x >0)
x + 5 là vận tốc là vận tốc lúc đi từ B về A
Thời gian mà người đó đi từ A đến B: \(\frac{60}{x}\) (h)
Thời gian mà người đó đi từ B về A: \(\frac{60}{x+5}\) (h)
Vì thời gian lúc về ít hơn thời gian đi là 1 giờ nên ta có phương trình:
\(\frac{60}{x}-\frac{60}{x+5}=1\) (ĐKXĐ: \(x\ne0\); \(x\ne-5\))
\(\Leftrightarrow\frac{60x+300-60x}{x\left(x+5\right)}=\frac{x^2+5x}{x\left(x+5\right)}\)
\(\Leftrightarrow x^2+5x-300=0\)
\(\Leftrightarrow x^2-15x+20x-300=0\)
\(\Leftrightarrow\left(x-15\right)\left(x+20\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=15\left(nhan\right)\\x=-20\left(loai\right)\end{cases}}\)
Vậy vận tốc của người đó đi từ A đến B là 15km/h

A B 50km 2h 30p x km/h x+2 km/h
Đổi \(30p=\frac{1}{2}h\)
Gọi vận tốc dự định của người đó là x (km/h) (x > 0)
\(\Rightarrow\) thời gian dự định của người đó là : \(t_{dđ}=\frac{S_{AB}}{v_{dđ}}=\frac{50}{x}\) (h)
Quãng đường ng đó di chuyển được sau 2 giờ là : \(2x\) (km)
\(\Rightarrow\)Quãng đường còn lại là \(50-2x\) (km)
Người đó phải tăng vận tốc thêm 2km/h trên quãng đường còn lại để đến B đúng dự định nên ta có PT :
\(\frac{50}{x}=2+\frac{1}{2}+\frac{50-2x}{x+2}\)
\(\Leftrightarrow\frac{50}{x}=\frac{5}{2}+\frac{50-2x}{x+2}\)
\(\Leftrightarrow\frac{50}{x}=\frac{5x+10+100-4x}{2\left(x+2\right)}\Leftrightarrow\frac{50}{x}=\frac{x+110}{2x+4}\)
\(\Leftrightarrow x^2+110x-100x-200=0\)
\(\Leftrightarrow x^2+10x-200=0\)
\(\Leftrightarrow\left(x-10\right)\left(x+20\right)\Rightarrow\orbr{\begin{cases}x=10\\x=-20\left(l\right)\end{cases}}\)
Vậy vận tốc ban đầu của xe là 10 km/h
Quãng đường AB dài là:
60 x 2 = 120 (km)
Nếu người đó đi với vận tốc 40km/h thì cần thời gian là:
120: 40 = 3 giờ

Gọi vận tốc ô tô dự định đi là v (km/h), (v > 3)
Thời gian đi 75 km đường đầu là 75/(v+2) (h)
Thời gian đi 120 – 75 = 45 km còn lại là 45/(v-3) (h)
Vì xe đến đũng thời gian dự định nên ta có phương trình:
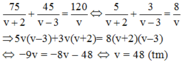
Vậy thời gian dự định là 120/48 = 2,5 giờ
Đáp án: A

Đặt ẩn x là vận tốc xe máy (x>0)
Lúc đầu đi vs x km/h thì lúc sau là x+9 km/h
Thời gian đi từ A -> B là 90/x thì thời gian từ B -> A là 90/x+9
Đến B còn nghỉ 30p=1/2h
Lập hệ phương trình thời gian:
(90/x)+1/2+(90/x+9)=5
<=> (90/x)+(90/x+9)=5-1/2
<=> (90.(x+9)+90.x)/x.(x+9)=9/2
<=> 90.x+810+90.x=(9/2).x.(x+9)
<=>180.x+810=(9/2)x^2+(81/2).x
<=> 0 = (9/2).x^2 - (279/2).x - 810
Gpt đc x=36 hoặc x=-5( loại vì ko thỏa mãn điều kiện)

Khi đó đoạn đường người đó đi với vận tốc 4km/h là 18 – x(km)
Thời gian đi với vận tốc 5km/h là x/5 giờ
Thời gian đi với vận tốc 4km/h là (18 - x)/4 giờ.
Vì thời gian đi hết đoạn đường không quá 4 giờ nên ta có bất phương trình: x/5 + (18 - x)/4 ≤ 4.
Ta có: x/5 + (18 - x)/4 ≤ 4
⇔ x/5 .20 + (18 - x)/4 .20 ≤ 4.20
⇔ 4x + 90 – 5x ≤ 80
⇔ 4x – 5x ≤ 80 – 90
⇔ -x ≤ -10
⇔ x ≥ 10
Vậy đoạn đường đi với vận tốc 5km/h ít nhất là 10km
chúc bạn học tốt :))