Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian người đó đi quãng đường đầu đó là :
\(t_1=\dfrac{s_1}{v_1}=\dfrac{3}{7,2}=0,42h.\)
Vận tốc trung bình người đó đi cả hai quãng đường là :
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{3+1,95}{0,42+0,5}=5,38\left(\dfrac{km}{h}\right)\)
Thời gian người đi bộ đi hết quang đường thứ nhất là:
v1 = s1/t1= 3000/2 = 1500 (m/s)
Thời gian người đi bộ đi hết quãng đường thứ 2 là:
t2 = 0,5 . 3600 = 1800 (m/s)
Vận tốc trung bình của người đó trên cả hai quãng đường:
vtb = (s1+s2)/(t1+t2) = (3000 + 1950)/(1500 + 1800) = 1,5 (m/s)

Thời gian của một người đi bộ đi trên quãng đường đầu
\(t_1=\dfrac{s_1}{v_1}=\dfrac{3}{7,2}=\dfrac{5}{12}\left(h\right)\)
Vận tốc trung bình của một người đi bộ đi trên cả hai quãng đường
\(v_{tb}=\dfrac{s_1+s_2}{t_1 +t_2}=\dfrac{3+1,95}{\dfrac{5}{12}+0,5}=5,4\left(\dfrac{km}{h}\right)\)

Đổi: \(2m/s=7,2km/h\)
Thời gian người đó đi quãng đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{3}{7,2}=\dfrac{5}{12}\left(h\right)\)
Vận tốc trung bình:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{3+1,95}{\dfrac{5}{12}+0,5}=5,4\left(km/h\right)\)
\(v_1=2m/s=7,2km/h\)
Thời gian đi trên quãng đường đầu là:
\(t_1=\dfrac{s_1}{v_1}=\dfrac{5}{12}\approx0,42\left(h\right)\)
Vận tốc TB là:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=5,38\left(km/h\right)\)
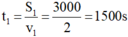
\(t_2=\dfrac{S_2}{v_2}=\dfrac{1,8}{10,8}=\dfrac{1}{6}h\)
\(\Rightarrow v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{3+1,8}{0,5+\dfrac{1}{6}}=7,2\) km/h